一、前沿
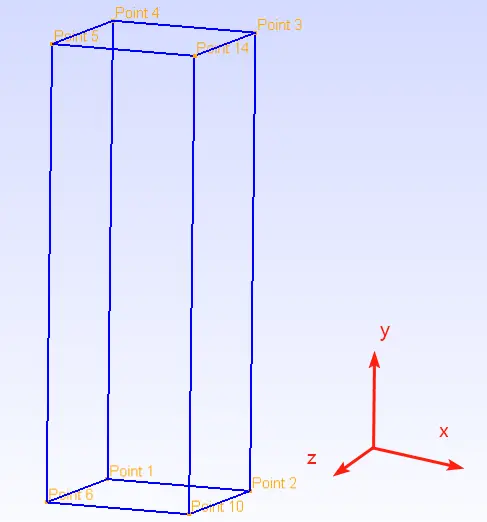
根据有限元分析(1)构建的长方形,我们继续研究网格划分问题。
根据有限元分析(2)我们知道了【挤压】命令
Extrude {0,0,0.12} { Surface{my_new_surfs[1]}; }
本节我们继续深入探索,网格划分细节
二、细节
1. 几何体(有限元分析(1))

2. 挤压成型---网格控制
【代码】
Include "t1.geo";
h = 0.1;
Extrude {0,0,h} { Surface{1}; }此时网格分析
控制网格划分:分层控制
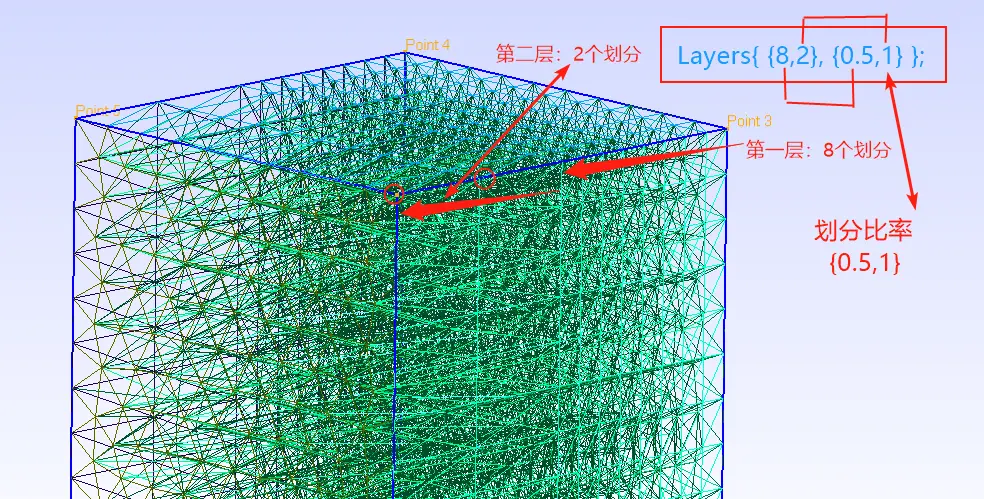
【代码】
Include "t1.geo";
h = 0.1;
Extrude {0,0,h} { Surface{1}; Layers{ {8,2}, {0.5,1} }; }3. 旋转挤压成型
旋转要素:旋转轴;旋转中心;旋转角度
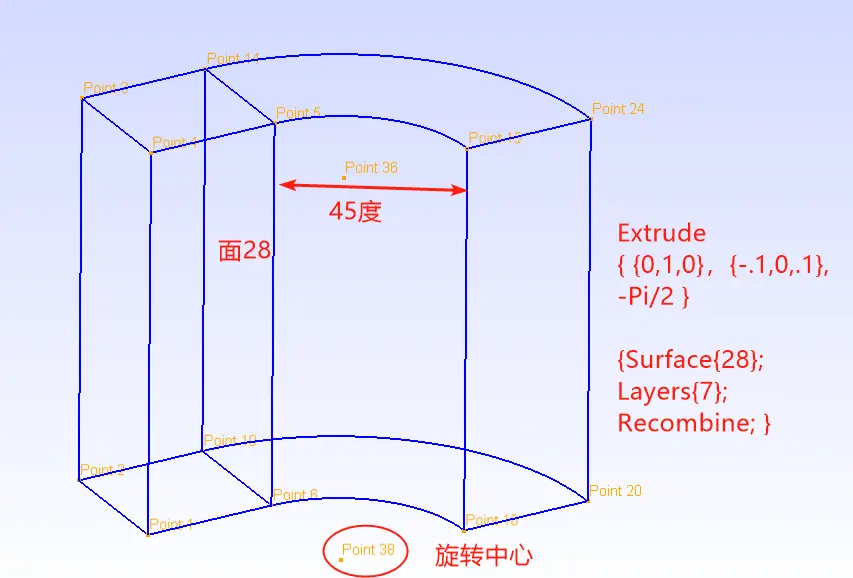
【代码】
Include "t1.geo";
h = 0.1;
Extrude {0,0,h} { Surface{1}; Layers{ {8,2}, {0.5,1} }; }
Extrude { {0,1,0} , {-0.1,0,0.1} , -Pi/2 } {
Surface{28}; Layers{7}; Recombine;
}网格探究
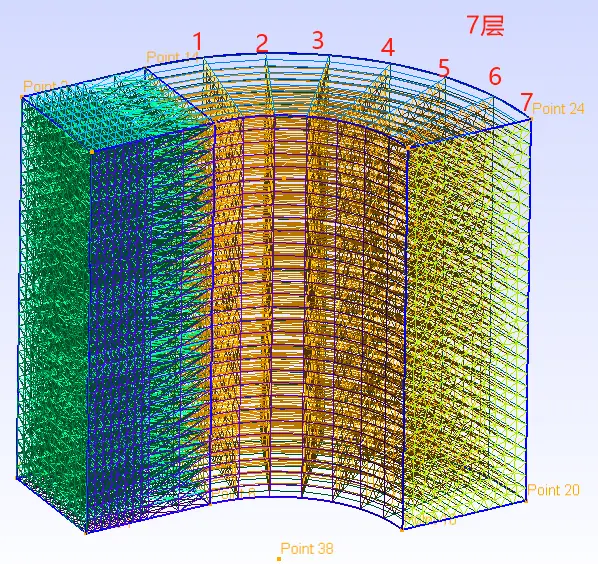
4. 引入新语法:定义参数
DefineConstant[ angle = {90, Min 0, Max 120, Step 1,
Name "Parameters/Twisting angle"} ];解释:定义角度常数列表;范围0-120;
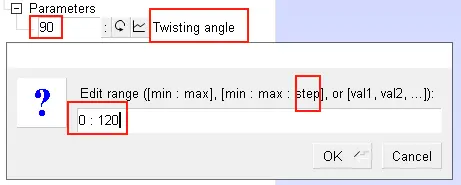
5. 移动与旋转同时挤压
Extrude { {-2*h,0,0}, {1,0,0} , {0,0.15,0.25} , angle * Pi / 180 } {
Surface{50}; Layers{10}; Recombine;
}
旋转角度探究
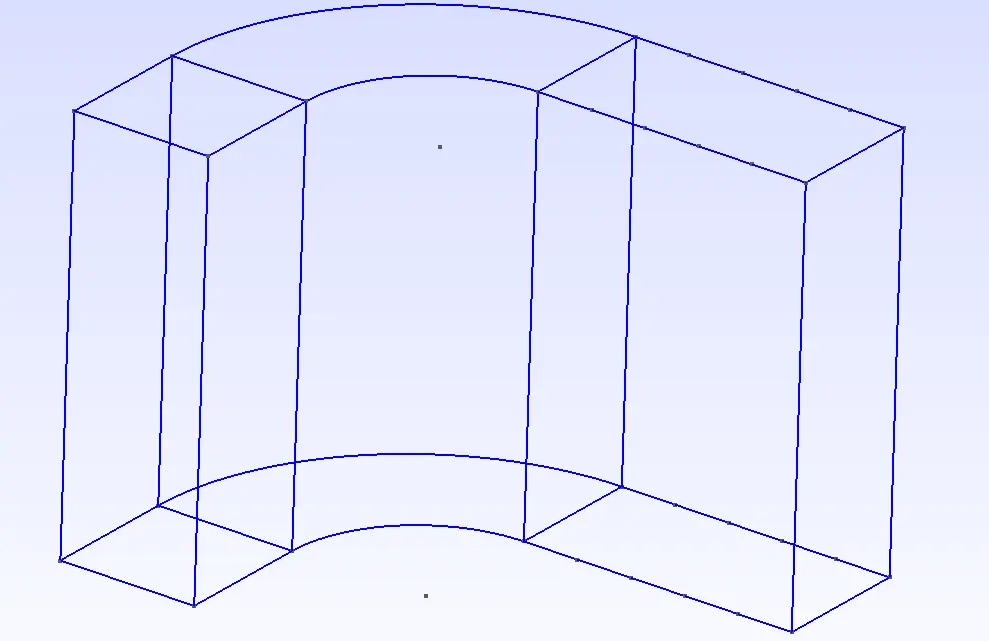
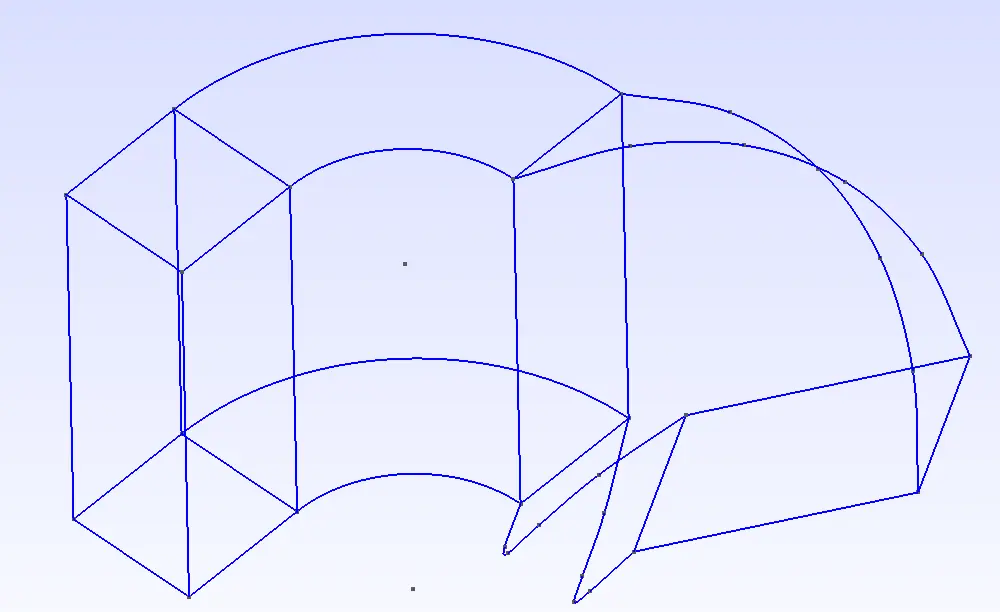
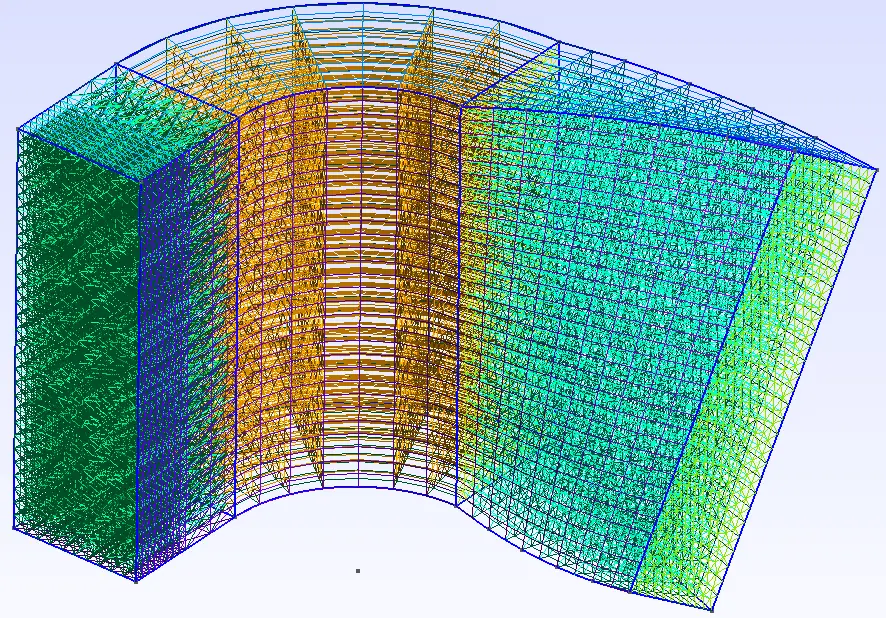
三、代码
Include "t1.geo";
h = 0.1;
Extrude {0,0,h} { Surface{1}; Layers{ {8,2}, {0.5,1} }; }
Extrude { {0,1,0} , {-0.1,0,0.1} , -Pi/2 } {
Surface{28}; Layers{7}; Recombine;
}
DefineConstant[ angle = {100, Min 0, Max 120, Step 1,
Name "Parameters/Twisting angle"} ];
out[] = Extrude { {-2*h,0,0}, {1,0,0} , {0,0.15,0.25} , angle * Pi / 180 } {
Surface{50}; Layers{10}; Recombine;
};
Physical Volume(101) = {1, 2, out[1]};
Geometry.PointNumbers = 1;
Geometry.Color.Points = Orange;
General.Color.Text = White;
Mesh.Color.Points = {255, 0, 0};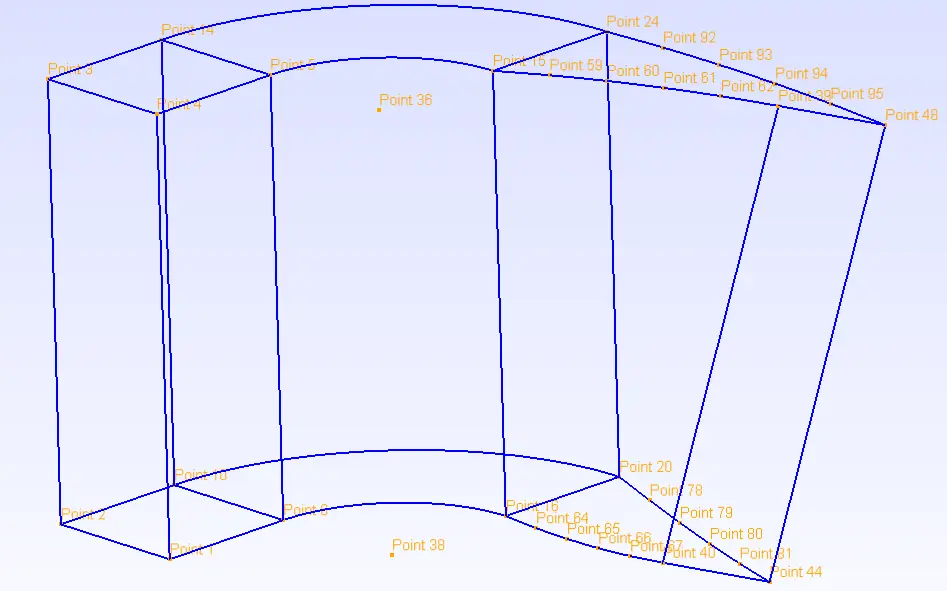
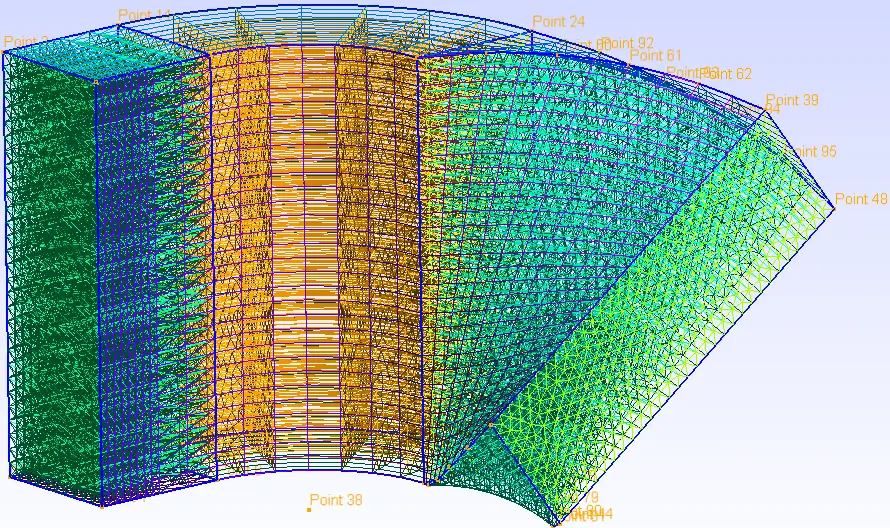
四、总结
我们在构建模型的时候,对网格进行了控制,以及参数的定义。这些新的知识使建模更加灵活,但是一次同时,增加我们的理解难度,只要我们一步一步的对代码剖析,总会发现背后的规律。
(1)挤压成型;可以沿着x,y,z挤压成型
(2)挤压成型:可以旋转成型
(3)挤压成型:既可以移动+旋转成型(如图13)
