一、前沿
根据有限元分析(1)讲解的几何体创建,我们只创建了一个长方形。比较简单,本次主要在长方形基础上,拓展形状,使形状更加复杂。
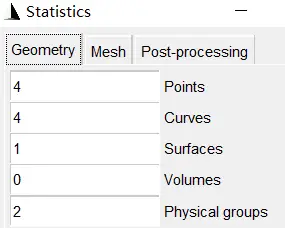
1. 有限元分析(1)形状如下
统计信息:
二、构建新的形状
构建的新形状如下:
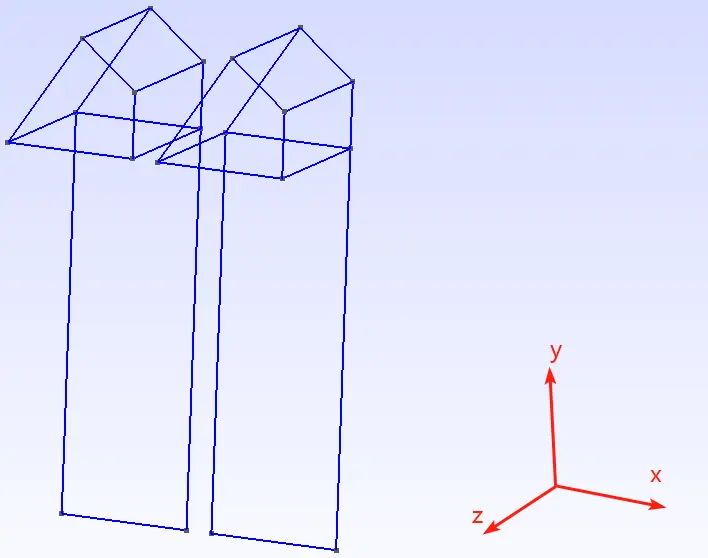
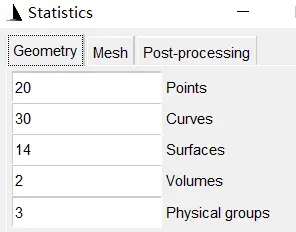
三、代码
Include "t1.geo";
Point(5) = {0, .4, 0, lc};
Line(5) = {4, 5};
// 点5, 向x轴负方向移动0.02大小
Translate {-0.02, 0, 0} { Point{5}; }
// {0, .4, 0, lc} --> {-0.02, .4, 0, lc}
// 点5 绕着点3 转轴为z 旋转 -Pi/4 角度
Rotate{{0,0,1}, {0,0.3,0}, -Pi/4} { Point{5}; }
// 点3 {0,0.3,0} 转轴z {0,0,1} 转动角 -Pi/4
// 首先复制点3;然后沿着y轴移动0.05
Translate {0, 0.05, 0} { Duplicata{ Point{3}; } }
Line(7) = {3, 6};
Line(8) = {6, 5};
Curve Loop(10) = {5,-8,-7,3};
Plane Surface(11) = {10};
// 首先my_new_surfs是一个列表(方括号)
// 列表存储的是 两个新表面的标签 my_new_surfs[0], my_new_surfs[1]
my_new_surfs[] = Translate {0.12, 0, 0} { Duplicata{ Surface{1,11}; } };
Printf("New surfaces '%g' and '%g'", my_new_surfs[0], my_new_surfs[1]);
Point(100) = {0., 0.3, 0.12, lc};
Point(101) = {0.1, 0.3, 0.12, lc};
Point(102) = {0.1, 0.35, 0.12, lc};
xyz[] = Point{5}; // Get coordinates of point 5
Point(103) = {xyz[0], xyz[1], 0.12, lc};
Line(110) = {4, 100}; Line(111) = {3, 101};
Line(112) = {6, 102}; Line(113) = {5, 103};
Line(114) = {103, 100}; Line(115) = {100, 101};
Line(116) = {101, 102}; Line(117) = {102, 103};
Curve Loop(118) = {115, -111, 3, 110}; Plane Surface(119) = {118};
Curve Loop(120) = {111, 116, -112, -7}; Plane Surface(121) = {120};
Curve Loop(122) = {112, 117, -113, -8}; Plane Surface(123) = {122};
Curve Loop(124) = {114, -110, 5, 113}; Plane Surface(125) = {124};
Curve Loop(126) = {115, 116, 117, 114}; Plane Surface(127) = {126};
Surface Loop(128) = {127, 119, 121, 123, 125, 11};
Volume(129) = {128};
Extrude {0,0,0.12} { Surface{my_new_surfs[1]}; }
//Extrude {0,0,0.12} { Surface{my_new_surfs[0]}; }
//Extrude {0,0,0.12} { Surface{1}; }
MeshSize {103, 105, 109, 102, 28, 24, 6, 5} = lc*3;
Physical Volume("The volume", 1) = {129,130};四、重点解释
1. Include "t1.geo";
代表将 "t1.geo" 文件中的内容复制到此文件
2. translate 【从这边 搬运 到那边】
Translate {-0.02, 0, 0} { Point{5}; }
具体含义:将点5,从原处 搬运到 另外一处, 搬运规则:沿着x轴负方向移动0.02个单位
3. Rotate 【使旋转,转动】
Rotate{{0,0,1}, {0,0.3,0}, -Pi/4} { Point{5}; }
具体含义:将点5 Point{5},进行旋转;规则:旋转轴为Z轴{0,0,1};旋转中心为 {0,0.3,0};旋转角度为 -Pi/4
4. Duplicata 【复制】
Translate {0, 0.05, 0} { Duplicata{ Point{3}; } }
复制点3;然后移动
5. Extrude 【(被)挤压出】
也可以理解为拉伸;创建体
Extrude {0,0,0.12} { Surface{my_new_surfs[1]}; }
将表面my_new_surfs[1]沿着z轴移动0.12后,挤压出体
五、网格分析
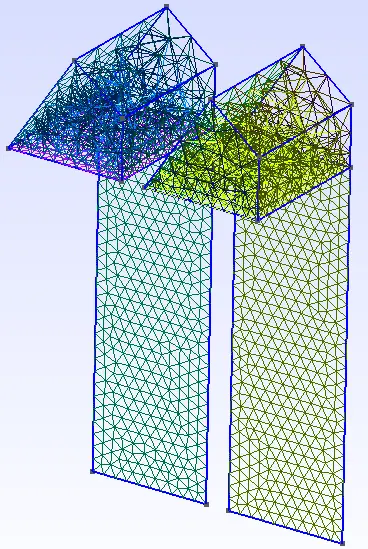
六、总结
经过前两节,我们基本上能够创建复杂的几何体,创建几何体的步骤:
点 -- 线(环) -- 面(面环) -- 体
Point -- Line -- Curve Loop -- Plane Surface -- Surface Loop -- Volume
上述建模方式虽然繁琐,但是我们能够知道更多的细节,也是看问题的一种方式。
此外:我们本节还学习了【移动】【旋转】【复制】【挤压】等命令,辅助建模,将如虎添翼。后续将创建更加复杂的模型。
参考文献
Gmsh官方文档的代码"t2.geo"
