热力学定律可以说是竞赛热学的重点考察对象,一开始学热学的时候就开始学它,然后做大量的气缸,循环之类的题目。我在一开始学它的时候,就会经常把一些概念搞混,不知道什么时候用什么表示,所以我认为明确定义是很有必要的,这也是我写这篇的一个小小想法(不然大家都会没什么好说的)。

零、热力学第零定律
热力学第零定律:在与外界影响隔绝的情况下,如果两个系统分别和处于确定状态的第三个系统达到热平衡,则这两个系统彼此也将处于热平衡 。
温度概念的导出:假设A与B,A与C均达到热平衡,则其状态函数p,V将受到制约
根据热零,B与C也处于热平衡,故也有
即这三个公式中只有两个是独立的,改写前两式
由于第三式不含VA,故等式双方的VA可以消去

代入第四式
等式左端仅含A的状态函数,故可用另一个函数fA表示
所以系统A,B,C互为热平衡时,一定存在一个状态函数是相等的,故定义其为温度。
一、热力学第一定律
热量:传递给一个物体的能量。
内能:分子动能和势能的总和,是一个态函数。
热力学第一定律:
在准静态过程中可写成
在定压条件下,可定义辅助函数焓:
热一的应用:绝热方程:
理想气体:

范德瓦尔斯气体,其内能函数表达式将在热二部分证明:
光子气体:
绝热大气模型:
二、热力学第二定律
热力学第二定律:用反证法可证明两种表述的等价性。
克劳修斯表述:不可能把热量从低温物体传到高温物体而不引起其它变化。
开尔文表述:不可能从单一热源吸取热量,使之完全变为有用的功而不产生其他影响。
用反证法可证明卡诺定理
卡诺定理:在相同的高温热源和相同的低温热源之间工作的一切可逆热机,其效率都相等,与工作物质无关。在相同的高温热源和相同的低温热源之间工作的一切不可逆热机,其效率都小于可逆热机的效率。
热力学温标:假设热源Θ1和Θ2,Θ1和Θ3,Θ2和Θ3之间存在三个可逆热机ABC,且A与B联合工作时等价于仅C工作,由卡诺定理有
由于等式左边不含Θ3,故右边的Θ3可以消去
若选择
则称其为热力学温标
克劳修斯不等式:假设一个系统相继与n个温度分别为Ti的热源接触最后回到温度为T1的热源,各热源放热为Qi,对外做的总功A=Qi,再假设有n个可逆热机分别工作于温度为T0和Ti的热源之间,使热源Ti吸热Qi(即Ti净放热为零),T0总放热为Q0,由热一和开尔文表述:
由卡诺定理:
当且仅当可逆循环时取等。n→+∞时化为环路积分:
即克劳修斯不等式。
克劳修斯熵:对可逆过程,克劳修斯不等式取等,有积分与路径无关:
故可定义态函数熵

熵增加原理:当热力学系统从一平衡态经绝热过程到达另一平衡态时,它的熵永不减少;如果过程可逆,则熵不变;如果过程不可逆,则熵增加。由克劳修斯不等式和熵的定义:

利用它可改写克劳修斯不等式:
熵定理:熵函数的存在,热力学温标的引进,熵增加原理的合称。
H定理:定义H函数
由微观过程可逆性
当且仅当细致平衡时取等,故平衡态为MB分布。
玻尔兹曼熵:不可辨别子系统的微观状态数相当于把Na个无差别的小球放入有差别的ga个盒子中,由于ga>>Na,单个盒子中的球不限个数与限制个数的极限相同(可辨别还要乘N!)
克劳修斯熵与玻尔兹曼熵的统一:
信息熵:
热二的应用1:理想气体、范德瓦尔斯气体,等体、等压、等温、绝热、多方,自由膨胀过程,过程方程、对外做功、吸收热量、内能变化、热容量、熵变的计算。下面不加证明地写出这些式子。
理想气体:

范德瓦尔斯气体:

热二的应用2:热平衡与自由能:
熵判据:在内能和体积不变的条件下,对于一切可能的变动来说,平衡态的熵最大。
自由能判据:在定温定体条件下,对于一切可能的变动来说,热平衡态的亥姆霍兹自由能最小。
在等温过程中,一个封闭系统所能做的最大功等于其亥姆霍兹自由能的减少。
自由焓判据:在定温定压条件下,对于一切可能的变动来说,热平衡态的吉布斯自由能最小。
在等温、等压条件下,一个封闭系统所能做的最大非膨胀功等于其吉布斯自由能的减少。
物体系内各部分之间的平衡条件:
热平衡:系统内部温度均匀。
力学平衡:系统内部压强均匀。
相平衡:系统内各相化学势相等。

有关相平衡和化学平衡的计算将在下一篇进行下次一定。
麦克斯韦关系:考虑二元函数全微分,有如下式子:
利用可逆过程中的克劳修斯不等式和热力学函数的关系,有
得到
以及麦克斯韦关系
与内能和物态方程的关系
利用它可计算范德瓦尔斯气体的内能表达式。
三、热力学第三定律
由于我看的物理书中没有热三的介绍,于是接下来我引用《物理化学》(南大)中的说明。
热力学第二定律只能告诉我们如何测量熵的变化值,但不能提供熵的绝对值。我们只能人为规定一些参考点作为零点,来求其相对值。这些相对值就称之为规定熵。其目的是为了便于计算∆S。零点在哪里呢?这就是热力学第三定律所要解决的问题。它是在非常低的温度下研究凝聚系统的熵变所外推出来的结果。
1902年T.W.Richard研究了一些低温下电池反应的∆H和∆G与温度的关系,发现当温度逐渐降低时,∆H与∆G有逐渐趋于相等的趋势。
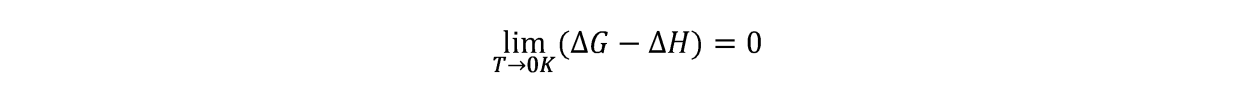
根据公式∆G-∆H =-T∆S,即使∆S≠0,当T→0K时,上式仍然成立。而根据
当T→0K时,上式成为0/0,这是一个不定式,从数学上讲∆S或∂∆G/∂T应都没有确定的数值。
1906年H.W.Nernst系统地研究了低温下凝聚系统的化学反应,提出一个假定:当温度趋于0K时,在等温过程中凝聚态反应系统的熵不变。
这个假定的根据是:从实验数据及∆H-T,∆G-T的图形,合理地推想在T→0K时,∆H与∆G有公共的切线,并且该切线与温度的坐标平行。这就是说在T→0K时,非但∆H与∆G趋于一致,并且∂∆G/∂T与∂∆H/∂T也趋于一致。
故得到Nernst热定理:在温度趋于热力学温度0K时的等温过程中,系统的熵值不变。
M.Planck在1912年把热定理推进了一步,他假定0K时,纯凝聚态的熵值等于零,承认Plank的假定,则热定理就成为必然的结果了。
Lewis和Gibson在1920年指出Planck的假定适用于完整的晶体。所谓完整晶体即晶体中的原子或分子只有一种有序排列形式(例如NO可以有NO和ON两种排列形式,所以不能认为是完整晶体,N2O和CO也是如此)。至此热力学第三定律可以表示为:在0K时,任何完整晶体的熵等于零。
1912年,Nernst根据他的Nernst热定理,提出了“绝对零度不能达到原理”,即“不可能用有限的手续使一个物体的温度冷到热力学温标的零度”。后来被认为是热力学第三定律的另一种表述方法。
Nernst热定理指出,在接近0K时,任何过程中的熵值不变,它既是等熵过程,又是绝热过程,没有热量的交换(如果有热量交换,∆S就不等于零)。因此,任何凝聚态物质在接近0K时,无论进行什么热力学过程,都不能通过释放热量而降低温度。又由于是凝聚态物质,也不能靠绝热膨胀对环境做功而降低温度。所以,系统的温度不可能继续降低,从而达不到绝对零度。
这部分最常见的就是理想气体状态方程,热一,热二在气缸,循环中的综合应用了。然而这里的难点应该是分布律,热一,热二,克劳修斯熵和玻尔兹曼熵的综合应用,应该好好理顺这些关系,熟练掌握公式的转换与运算才能在各大机构出的奇葩题目中存活。