说起韦达定理,可能会有人嗤之以鼻:“不就是给出了二次方程根与系数的关系吗?谁不会啊?求根公式我会推,一加一乘不就有了?要是我生早一点,就是我的定理了。”
啊哈,实际上韦达定理并没有你想象的那么简单,也没有你想象的那么难(封面),我敢打保票,在座的都能理解。

在我们的数学课本里,教材是怎么得到韦达定理的?是先求出求根公式,然后一加一乘就出来了。然而,韦达定理并不是这样推导得来的,教材的“推导”只能算是“验证”,很容易误导学生。
我问你,一元三次方程根与系数的关系是多少?你是不是还想像教材那样去加、乘?我把求根公式(还是特殊简单形式)给你看一下:
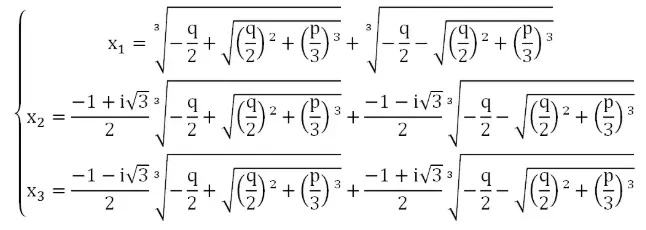
来来来,笔给你,你来算。来啊,你算啊,怎么不算了啊?你不是要算的吗?
诶,你看,这个时候,我们教材的方法已经不适用了。实际上,三次方程的求根公式是根据韦达定理推导得来的。也就是,在三次方程求根公式出来之前便已经有了三次方程的韦达定理,并且三次方程求根公式是建立在韦达定理之上的。
韦达的厉害之处就在于,他提出了二次、三次方程根与系数的关系,并且按照他的思路,我们可以推导到四次五次乃至n次。

首先,为什么韦达定理是两个根相加,相乘,而不是相减相除呢?因为,如果是减法除法的话,你把两个根的值调换,得到的结果就不是一个固定值,起码得加上正负号,那会十分麻烦。
举个例子。比如说二次方程x²=4的两个根分别是2,-2.
OK,x1+x2=2+(-2)=0。
x1-x2呢?x1-x2是不是可以是2-(-2)=4,也可以是-2-2=-4?它们的值是不一样的。你看,这样子我们就无法用一个常数来表示x1-x2。
x1÷x2也是如此。x1+x2和x1x2不管怎么调换,值都是不变的。

我们不要去想求根公式,先看看二次方程ax²+bx+c=0(a≠0)根与系数的关系。
我问你,对于这个方程,能不能满足(x-x1)(x-x2)=0?x的值是x1和x2中的一个,如果是x1的话,x1-x1=0,0乘任何数都得0,成立;如果是x2,x2-x2=0,0乘任何数都得0,仍然成立。
所以,(x-x1)(x-x2)=0是成立的。那么,我们不妨把它给展开(你不妨在草稿纸上算一下):
(x-x1)(x-x2)=0展开后是x²-xx2-x1x+x1x2=0。
整理一下,有:
x²+(-x2-x1)x+x1x2=0
对照原方程,我们发现还少了a。等式两边同乘a得:
ax²+a(-x2-x1)x+ax1x2=0
它与原方程是同时成立的。对照原方程的系数:
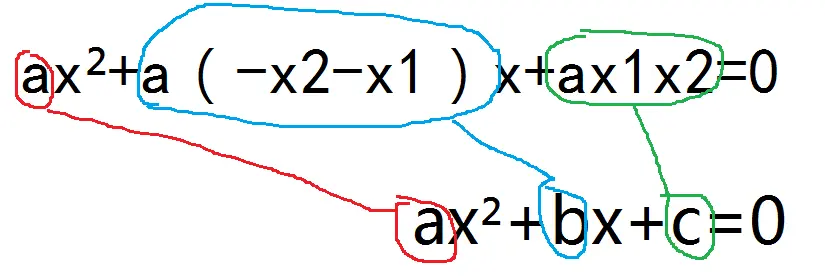
我们发现,这两个式子每一项的系数是可以对应起来的。
a对应a,a(-x2-x1)对应b,ax1x2对应c。
因为这两个方程是同时成立的,也都等于0,系数也能一一对应,这也就说明,它们对应项的系数是相等的。让a(-x2-x1)=b,ax1x2=c的话,上面的式子就能变成下面的式子。
因此我们可以得到:
a(-x2-x1)=b,ax1x2=c
那么x1+x2和x1x2的值便显而易见了。于是有:
x1+x2=-b/a,x1x2=c/a。
这就是我们熟知的韦达定理。

我们再来看看三次方程的韦达定理。
三次方程的一般形式为:ax³+bx²+cx+d=0(a≠0)。
我们依然可以得到:(x-x1)(x-x2)(x-x3)=0.
我们把上式再次展开,得到:
x³+(-x1-x2-x3)x²+(x1x2+x1x3+x2x3)x+(-x1x2x3)=0
等式两边同乘a,得到:
ax³+a(-x1-x2-x3)x²+a(x1x2+x1x3+x2x3)x+a(-x1x2x3)=0
这个等式依然可以和原方程对应起来:
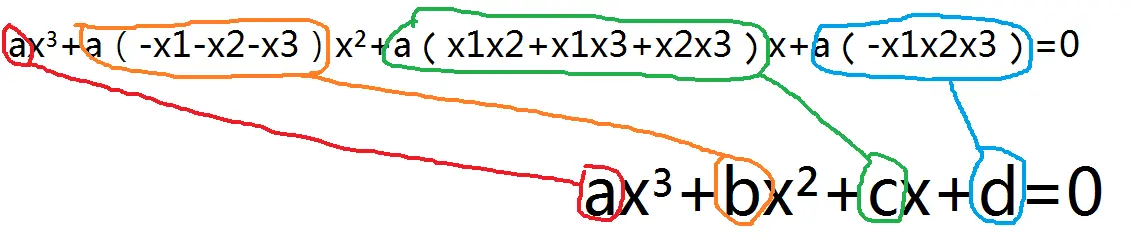
于是我们有:
a(-x1-x2-x3)=b,a(x1x2+x1x3+x2x3)=c,a(-x1x2x3)=d
也就可以得到:
x1+x2+x3=-b/a,
x1x2+x1x3+x2x3=c/a,
x1x2x3=-d/a
你看,我们不需要用到那吓人的求根公式,我们也能得出三次方程根与系数的关系。

二次方程根与系数的关系为:
x1+x2=-b/a,
x1x2=c/a
三次方程根与系数的关系为:
x1+x2+x3=-b/a,
x1x2+x1x3+x2x3=c/a,
x1x2x3=-d/a
发现了什么规律了吗?单看等式右边,先看符号,-+-···,分子是b,c,d···。这是有规律的。这个规律我不好总结,有兴趣的朋友推荐去看李永乐老师的视频。
根据这个规律,我们可以得到一般n次方程
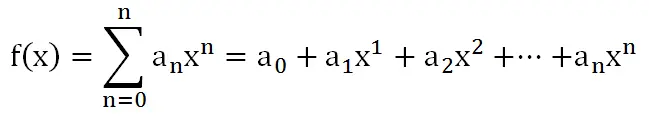
根与系数的关系。
当然,n次方程就会有n条根与系数的关系,凭我的能力,完全表示不出来。这里有一个看规律版的:
你看啊,右边是-+-+-+···,分母都是an,分子的下标则是有规律的n-1,n-2,n-3···;左边的式子也是有规律的。
对于我们的四次五次n次方程,我们依然可以沿用韦达的方法,去求出根与系数的关系。
PS:要看三次四次求根公式的可以去我的空间里翻,视频专栏都有。
