基本概念
机器学习就是让机器具备找一个函数的能力。
这句话强调了机器学习的核心任务是通过数据训练来发现和优化一个映射输入到输出的函数(模型),让机器在非预设条件下能够根据某种逻辑推导数要调用的方法,即函数。这使得计算机能够根据从数据中学到的模式,对新的数据进行预测或分类。
例如,垃圾邮件检测。我们希望找到一个函数,它可以将电子邮件的特征(如关键词、发送者等)映射到“垃圾邮件”或“正常邮件”的标签上。机器学习模型(如支持向量机、决策树)会从已有的标记数据中学习,找到适合的分类函数。
机器学习的任务
回归(regression)
假设要找的函数的输出是一个数值,一个标量(scalar),通过分析现有的数据,进行归纳总结,确定输出的值。
分类(classification)
分类任务要让机器做选择题。人类先准备好一些选项,这些选项称为类别(class),现在要找的函数的输出就是从设定好的选项里面选择一个当作输出,该任务称为分类。
结构化学习(structured Learning)
机器创造一些有结构的东西(image,document)
机器学习找函数的过程
以视频的点击次数预测为例介绍下机器学习的运作过程。
step1 写出一个带有未知参数的函数 f
写出一个带有未知参数的函数 f,其能预测未来观看次数。比如将函数写成
y = b + wx1
y 跟 x1 都是数值,b 跟 w 是未知的参数。以上为一个猜测,来自于关于这个问题的领域知识(对这个问题本质上的了解)。
1、带有未知的参数(parameter)的函数称为模型(model)。
2、特征(feature) x1 是这个函数里面已知的信息,.
3、w 称为权重(weight),b 称为偏置(bias)
step2:定义损失(loss)
损失函数指的是在机器学习中用来衡量模型预测结果与实际结果之间差异的函数。其值越小,代表模型预测结果越接近实际结果。在训练模型时,需要通过不断调整模型参数来最小化损失函数的值。
在这个例子中,损失函数 为L(b, w),这个函数的输入是模型里面的参数b 跟w。从训练数据来计算损失。
具体步骤:
1、假设未知的参数的设定是 b = 500,w = 1
2、代入某一具体数据x1得估测值yˆ
3、计算一下估测的值 yˆ 跟真实值 y 的差距 e
4、求平均误差L
计算差距的方法:
1、平均绝对误差(MAE)
e = |yˆ − y|
2、均方误差(MSE)
e = (yˆ − y)2
3、交叉熵(cross entropy)
有一些任务中 y 和 yˆ 都是概率分布,这个时候可能会选择交叉熵(cross entropy)。
误差表面(error surface)
试了不同的参数,计算它的损失,画出来的等高线图(二维)
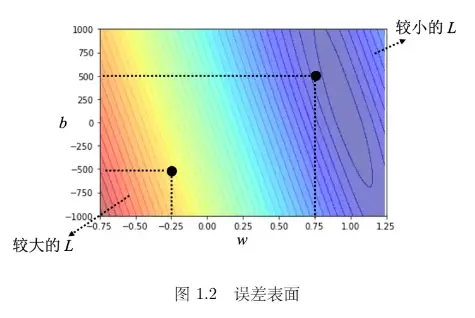
step3:解一个最优化的问题
找到让损失最小的w和b代表它们是最好的一组。
最常使用的优化方法:梯度下降
梯度下降是一个常用的优化算法,用于求解目标函数的最优解或局部最优解。它通过不断调整模型参数的值,使目标函数的值逐渐下降。具体来讲,每次迭代时,它计算目标函数的梯度(即函数在当前点处的斜率),并朝着梯度的反方向更新参数值,以使函数值下降。这个过程一直持续到目标函数的值收敛(即不再变化或变化极小)。此时,算法得到的参数值就是目标函数的最优解或近似最优解。
影响寻找最优解速度的因素:
1、斜率大小
2、学习率(learning rate)η (自己设定),影响参数更新的量
假设只有一个未知的参数 w,b 是已知的。w 代不同的数值的时候,就会得到不同的损失,这一条曲线就是误差表面(一维)。
损失函数可以为负,由自己定义。
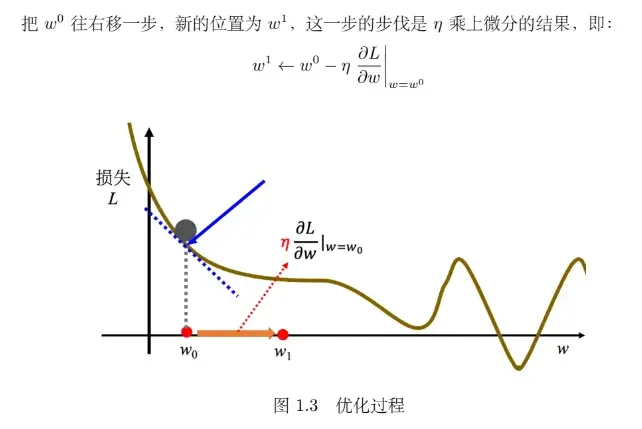
接下来反复进行刚才的操作,计算一下 w1 微分的结果,再决定现在要把 w1 移动多少,再移动到 w2,再继续反复做同样的操作,不断地移动 w 的位置,最后会停下来。
何时停止计算?
1、达到设计的参数更新次数上限
(更新次数和学习率都是超参数)
2、当调整参数到一个地方,该处微分的值为0,参数停止移动位置
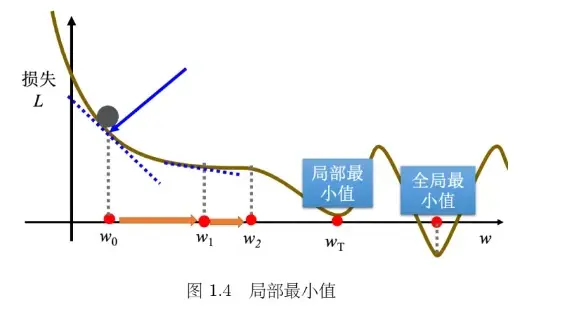
梯度下降方法存在的问题:
当找到局部最小值时停止训练,我们真正要寻找的是全局最小值。
在两个参数的情况下使用梯度下降:
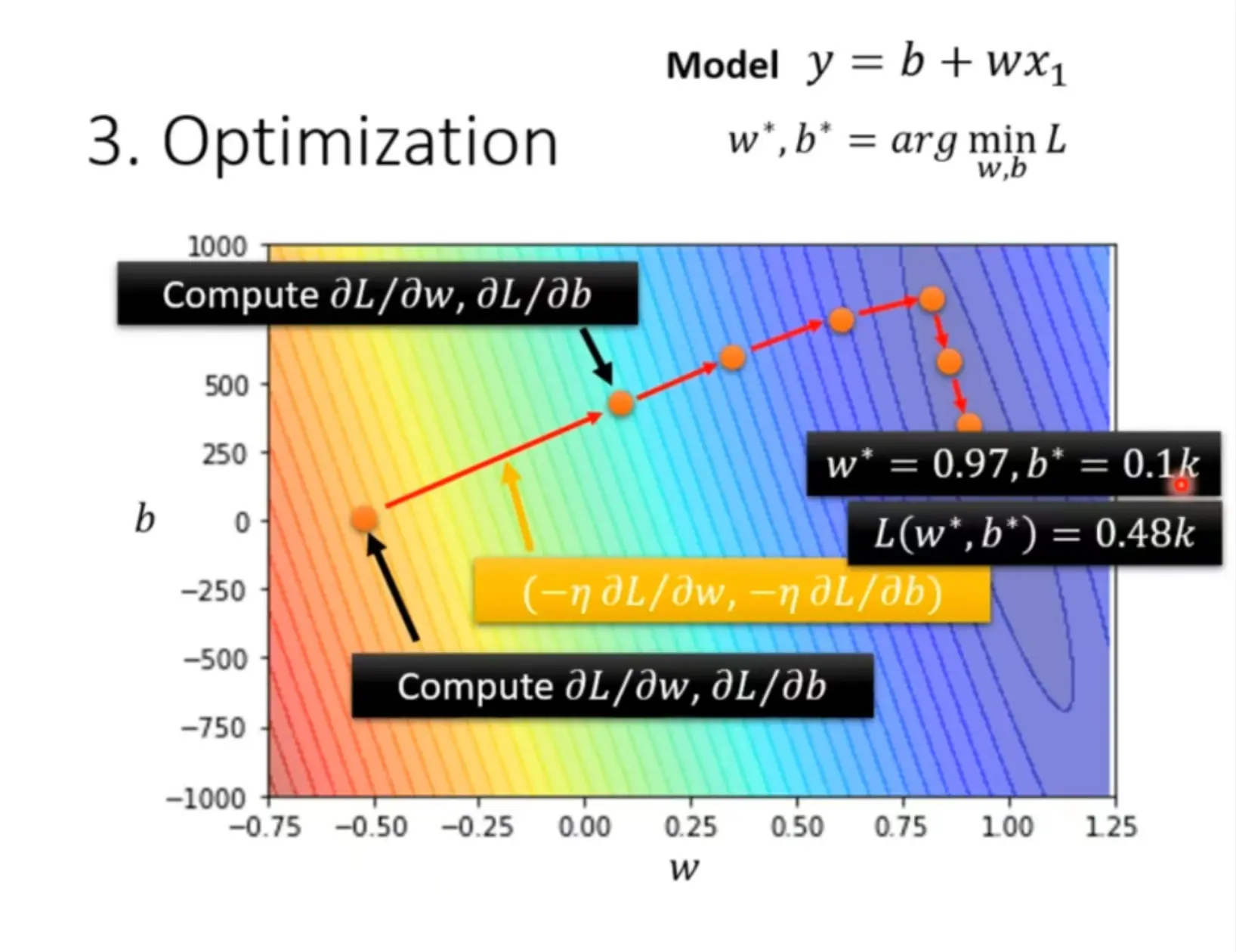
术语总结
机器学习:机器能像人一样,在接受一定的信息后,能够找到反应事物之间关系的规律,通过函数去反映,能够预测同一类事件未产生的结果。
回归:找到的函数对现有的数据进行分析、归纳、总结,得到一个具体的标量数值。
分类:函数输入不同类别的信息,进行区分,输出其中的一类信息。
结构化学习:函数输入一定信息,寻找其中的逻辑,而不是简单的分析数据关系,输出具有一定结构的东西。如图片,文章。
参数:描述当前问题中各变量之间关系的量。
模型:带有一系列未知的参数的一组函数。
特征:函数中已知的,输入的信息。
权重:衡量特征值重要程度,用数值做系数反应重要程度大小。
偏置:对特征值预设的偏好或倾斜。
梯度下降:通过计算函数当前点的梯度,朝着梯度相反方向更新参数值,使目标函数的值一直下降,持续到目标函数的值收敛,即找到目标函数的最优解或近似最优解。
学习率:模型的参数更新时,每次改变的量的大小。
超参数:人为提前设定,而非机器产生的参数。
