上周没发视频,是因为高估了自己的计算能力
上周研究的课题是这样的:一个尺寸为n*n(n是偶数)的正方形平面,随机方向密铺1:2的矩形。理论上,可以正好不留缝隙的铺满。如同下面这样,10*10的空间内,1:2的矩形随机铺满。

我本来觉得找到合适的解决方案并不是特别难,从周四开始研究,做着做着觉得自己可能搞不定,然后又求助于AI,经过和ChatGPT以及Claude的多次探讨,仍然没有得到满意的结果……一直到今天,也并没有得到一个完全满足预期的结果。
为什么要发这个专栏呢,一个是虽然没有完全满足预期,但还是鼓捣出一个只差一行的方案来。
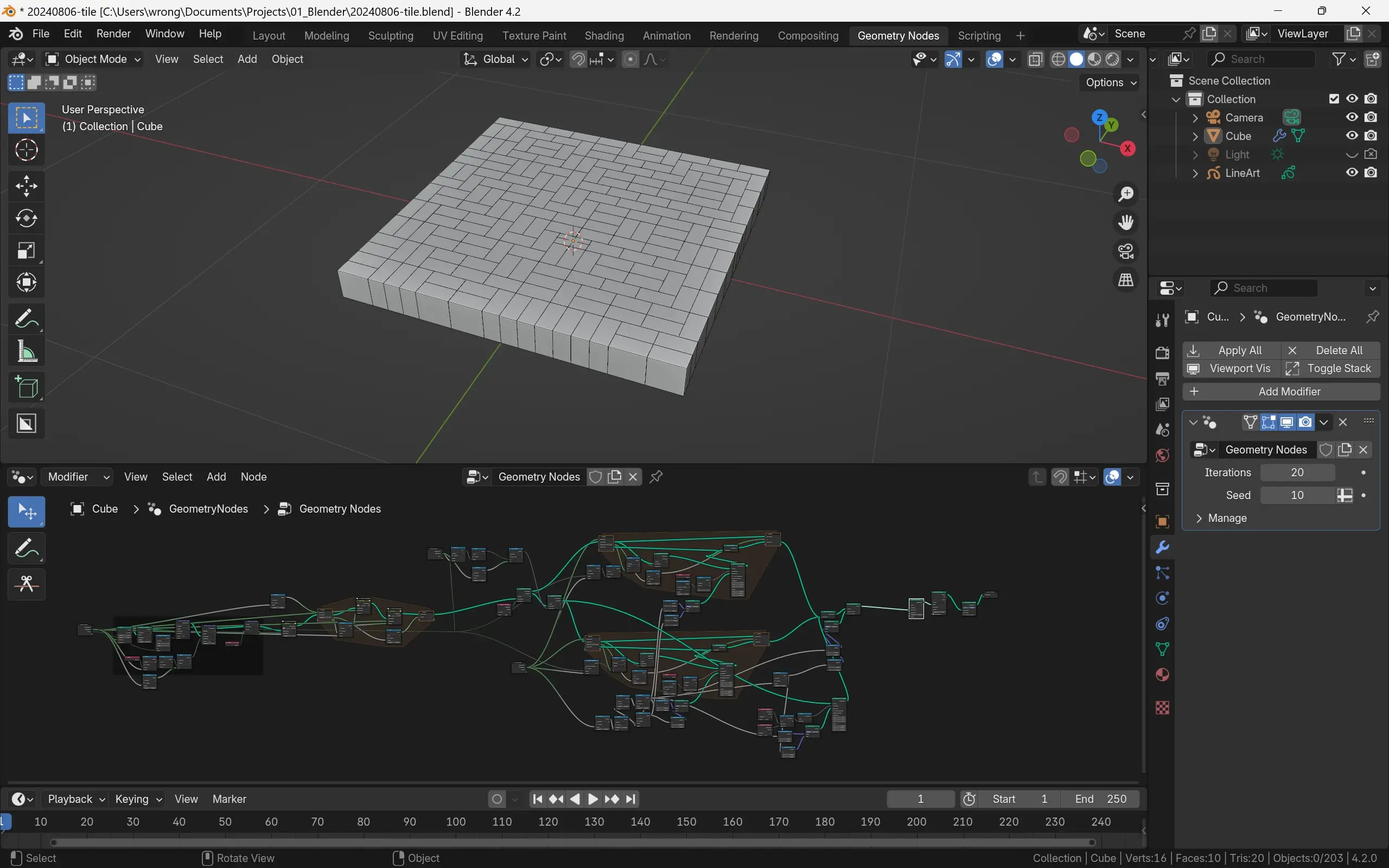
这个方案,在60%以上(比例应该大于60%)的情况下是有效的,但有不小的概率出现最后一行必须填充偶数个1:1的正方形
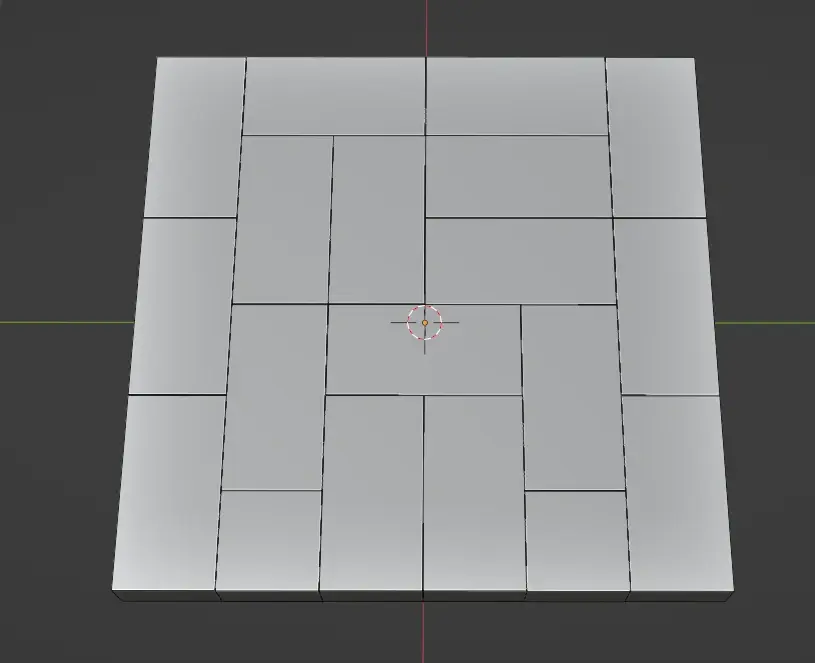
比如6*6的情况下,随机数取值为0的时候,最后一行(最下面这行),就出现了两个1:1的块。按逻辑来说,最后出现横向块断开的情况,应该在这些块所在的矩形区域重排,如下图这样。
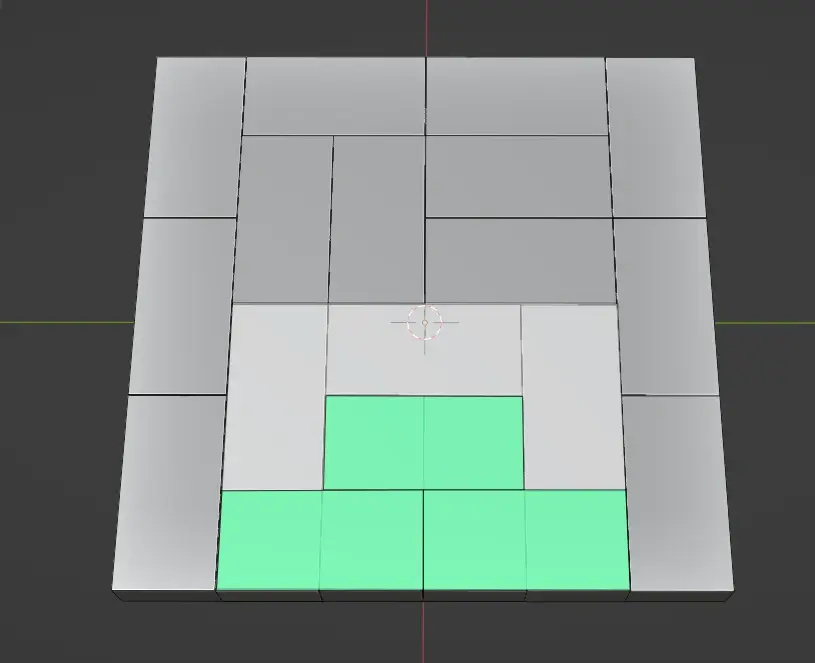
但用我的方法做这个嵌套就过于复杂了,已经超出我的理解范围。
所以这也是发这个专栏的第二个目的,求助一下,不知哪位同学有更完善的方案来解决这个问题呢?请不吝赐教。
——当然我也会继续优化自己的方案,视频估计就不录制这个计算过程了,过后会用这个模型做点其他动画,敬请期待。
