
Heise method是一种相对小众但效率很高的魔方解法,它能在不借助任何公式、不尝试多种可能的情况下,平均在40步内复原三阶魔方(语出Sebastiano Tronto,Fewest Moves Tutorial),其思路对于魔方最少步项目(Fewest Moves Challenge,FMC)特别有借鉴意义,同时也发展出了可应用于速拧的Speed-Heise公式集(作者Matt DiPalma,详见https://www.speedsolving.com/wiki/index.php/Speed-Heise)。
Heise method作者Ryan Heise的网站(https://www.ryanheise.com/cube)有该法详细文字教程和一些魔方知识(包括转换机、筑块、降群原理等),以及诸多动图(是虚拟魔方播放器,不是gif动图,但本文只能用gif形式截取,因此墙裂建议访问原站,体验更佳)。目前Heise method中文资料较少,网页机翻又词不达意,于是我一面学习,一面便想斗胆做一些翻译和整理。
本系列专栏中,我将意译Heise method(下称“Heise法”)教程全文,同时夹带私货(算是学习笔记,会用蓝字标注出来的XD)。水平有限,还望魔友们多多指教~

本节将介绍一些基本的魔方理论(触及魔方的数学本质了)。理解一些魔方的基本性质将帮你判断哪些操作是可行的,哪些是不可能的,并协助你找出“更优雅的”魔方复原方法。
1. 基本定义(Basic definitions):了解三阶魔方的结构、Orientation和Permutation
2. 魔方的法则(Laws of the cube):了解什么是“合法的”操作及其限制
3. 对称关系(Symmetry):一些看似不同的情形有着相同的本质
4. 群论(Group theory):熟悉魔方的若干子群(Subgroup)及其性质
5. 循环(Cycles):了解循环及其应用
6. 奇偶性(Parity):了解奇偶性/奇偶校验,以及它可能导致的问题
为保证原教程逻辑畅通同时控制篇幅,本节先讲逻辑联系最紧密的第1、2、4点。Enjoy~

1. 基本定义Basic definitions
把三阶魔方拆了(不拆魔方,亦可练功),你会发现它由21个部件组成:
◆12个棱块,每块有2个颜色
◆8个角块;每块有3个颜色
◆1个中轴,有6个面(所以6个面6个中心颜色的相对位置是不可改变的,这与偶数阶魔方不同)。
下面请看这两个单词:
Orientation(n.)目标,定位;方向,朝向;(基本的)态度,倾向;(岗前、学前、课前等的)情况介绍,培训;适应,熟悉
Permutation(n.)[数] 排列;[数] 置换(摘自dict.youdao.com)
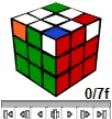
◆Orientation在魔方中指色块的朝向,也指把色向调整正确的过程(俗称O,就是OLL的O)。例如下图中白色中心块所在面,只有一个角块白色朝上,其他三个角块的色向是错误的。使用经典的7步“小鱼公式”可将色向朝整正确。
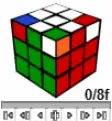
◆Permutation在魔方中指色块位置的排列,也指把位置调整正确的过程(俗称P,就是PLL的P,有时也简称Perm)。Permutation不一定要考虑色向,例如下图过程只调整正确了三个角块的位置(进行Corner Permutaion,CP),但它们色向不正确(没有Corner Orientation,CO)。
PS:下文“群论”中,Permutation同时包含色向和位置信息(为了和这里的Permutation区分,我称之为狭义Permutaion)。
鉴于Orientation和Permutation两个术语在魔方领域流传甚广、意义复杂,为了表达的准确和简明,一些句子中我将保留这两个英文单词不作翻译。还请读者记住这两个单词。
2. 魔方的法则Laws of the cube
先了解一下UP主「魔方达人夏天」这波操作的含金量!「BV17M411V7Nz」
视频加载失败

为什么在这里放这个呢?请看下文——
一个有趣的事实是,如果你把三阶魔方拆散后随机组装,能正常复原的概率只有1/12(正常复原,是指只通过“合法的”转动复原,即不把魔方再次拆开)。为什么呢?
(1)合法转动只能实现1/2的Permutation(这里不考虑Orientation)
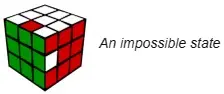
事实证明,面对一个打乱的魔方,每次只拆两个棱块或两个角块下来,对换位置装上,直至魔方复原,一个合法状态的打乱一定会在偶数次“两两对换”后复原,而不可能是奇数次“两两对换”(若把偶数次的和奇数次的视作两个集合,这两个集合互为补集)。
为什么呢?且看下方例子,想象下图是三阶魔方的某个面,它顺时针转动了90度:
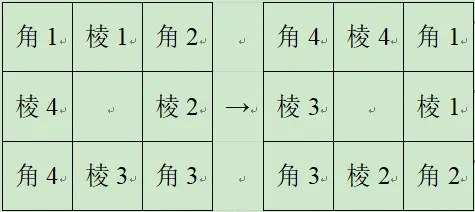
如果通过两两拆装对换的方式,从左边状态到右边状态等价于6次对换(角1-角4,角1-角3,角1-角2;棱块同样有3次,共6次,是偶数)。

因此每一次转动都相当于发生偶数次对换,而不断打乱就是偶数的叠加,仍是偶数。
一个拆散后随机组装的魔方,有偶数次或奇数次对换的可能性各半,因此说合法转动只能实现1/2的Permutation。
(2)合法转动只能实现1/2的EO(Edge Orientation)
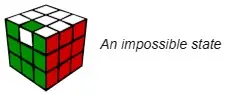
事实同样证明,一次合法转动一定会改变偶数个棱块的色向;如果魔方上存在色向错误的棱块,错误的个数一定是偶数。上图的情况显然绝无可能通过合法转动复原。
但如何判断一个棱块色向正确与否?一个最常见的框架是这样:如果一个Permutation错误的棱块只通过L、R、U、D层的转动即可回到正确位置,那么这个棱块的色向就是正确的。在此框架下,L、R、U、D层的转动影响0个棱块的色向,而F、B层每次转动都影响4个棱块的色向。0和4都是偶数,因此合法转动不可能影响奇数个棱块的色向(拿起手边的魔方,只使用L、R、U、D单层转动打乱它,看看会发生什么?)。
浅浅引入一下“颜色分级”的概念。如果保持白顶绿前坐标,规定U、D面为“高级面”,白色和黄色为“高级色”;F、B面为“中级面”,绿色和蓝色为“中级色”;L、R面为“低级面”,红色和橙色为“低级色”。
对于只使用L、R、U、D层转动打乱的魔方,可以发现:每个棱块上都符合“较高级面上的颜色比较低级面上的颜色等级更高”,也就是说U、D面不可能出现红色、橙色,L、R面不可能出现白色、黄色……
读完后文的“群论”再来看这一段,会更有体会。
(3)合法转动只能实现1/3的CO(Corner Orientation)
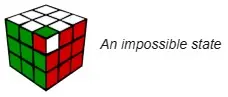
至于角块,每个角块有三个面,也就是三个可能的色向,解释起来会比棱块稍难。让我们给角块的三个色向赋值:正确色向为“0”,相对于正确色向原地顺时针翻转一下为“1”,相对于正确色向原地顺时针翻转两下(即逆时针翻转一下)为“2”。事实证明,合法转动引起角块色向值变化量的总和一定是3的整数倍。上图中发生的色向值变化量为1,不能被3整除。
角块色向的框架是这样的:规定每个角块带有顶面或底面颜色的一面朝向顶面或底面时,该角块色向正确(简单说就是,假如固定魔方坐标,白色为顶、黄色为底,那么一个角块上的白色或黄色贴纸只要朝向顶面或底面,这个角块的色向便是正确的;再看上图“不可能”的情况,白色贴纸相对于正确位置进行了一次顺时针翻转,所以它的色向值为“1”)。这个框架下,转动U、B层不影响角块色向,色向值变化量为0;而L、R、F、B层每进行一次90度转动就会影响4个角块的色向,其中2个角块由“0”变为“1”,2个角块由“0”变为“2”,其余4个角块保持“0”色向,总和就是1+1+2+2+0*4=6,6是3的整数倍。
为什么角块色向值变化量一定是3的整数倍而不是6的整数倍呢?可以想想层先法顶层十字完成后,调整顶层角块色向时可能遇到的7种case,其中Sune的色向值变化量不就是3么?
综上所述,如果魔方是拆开随机重装的,只有1/12(1/2 * 1/2 * 1/3)的状态可通过合法转动实现。
再回去看UP主夏天的骚操作,其实是将两个棱块拆下来对换了。
4. 群论Group theory
魔方的数学本质上可用“群”的概念来理解和描述。一个群由许多元素组成,对魔方而言,一个Permutation就是一个元素(这里的Permutation包含了Orientation概念,为和上文区分,我称之为“狭义Permutation”;所以魔方的所有4.3×10^19种状态都是互异的元素)。群具有以下性质:
①封闭性(Closure):一个群中有两个Permutation,分别是P1和P2,那么P1•P2(做完P1后接着做P2)所得结果仍在同一个群中(数学语言:对任意a,b∈G,有a•b∈G)。
②结合律(Associativity):P1•(P2•P3)与(P1•P2)•P3结果相同(数学语言:对任意a,b,c∈G,有a• (b•c) =(a•b) •c)。
③存在单位元(Identity):一个群中必存在一个元素是魔方的复原状态(数学语言:存在元素e∈G,使得对任意a∈G,有a•e=e•a=a;这里的e指单位元,即魔方复原状态)。
④存在逆元(Inverse):一个Permutation的逆序也在同一个群里(可理解为某情况的逆打乱;数学语言:对任意a∈G,存在a^(-1)∈G,使得a•a^(-1)=a^(-1)•a=e)。
对魔友们而言,最有趣的性质大概是封闭性,它意味着如果只选择一个子群中的操作,魔方就会保持在这个子群的状态中。
下面是两个在各种魔方解法中都比较常见的子群:
◆#1 <U D R2 L2 F2 B2>
假如有一个这样生成的群:U、D层允许90度和180度转动,其他层只允许180度转动。如果你根据这个限制条件打乱魔方,魔方的白色和黄色贴纸一定会保持朝上或朝下,中层棱块也会保持色向正确(相当于2*3*3多米诺魔方的转动方式)。
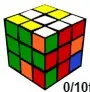
其实这个状态正是“多米诺降群法”(Domino Reduction,DR)第一步的结果。多米诺降群法是常用于最少步数解的一种方法,也就是把完全打乱的魔方<U D R L F B>(即“乱群”:在绝对坐标系下,魔方按照任意步骤打乱后,魔方块产生变化的位置的集合——引自UP主天方魔「BV1oA411f7nD」)进行一步“降群”,变成侧面只转180度即可复原的状态<U D R2 L2 F2 B2>。
◆#2 <U D R L F2 B2>
Heise法中利用到的一个有趣的群是通过限制F、B层只允许180度转动生成的,这个群符合上文“魔方的法则”中的棱块色向框架(ZZ法和盲拧四步法也都用这个群限定棱块色向)。

再次剧透一下,Heise法流程大致是完成F2L-1——差一个空槽完成的前两层——并调整棱块色向,再复原余下部分。在调整色向之后,只要限制F、B层只进行180度转动,就能很容易地保持棱块色向不受破坏。

Ryan Heise在2002年曾研究过把计算机解魔方算法“降群法”移植为人工操作的方法,即Human Thistlethwaite Algorithm(详见https://www.ryanheise.com/cube/solutions.html)。详见本文集【番外篇】~
可以求个赞么~这是对我莫大的鼓励!
