为什么标题就只能这么长啊。可能很多人都知道机器学习领域,特别是神经网络的涌现能力了。不过这篇文章研究的涌现有些不一样,在训练过程中,作者发现transformer模型完全学会了用傅里叶变换解决同余加法问题:


1.涌现
还是先介绍涌现。
为什么我觉得大模型值得研究呢?一个很神奇的点就是涌现。我专栏中也经常提到这一点(虽然不一定用的这个词)
这组图很好的说明了涌现。在模型的规模没有达到一定规模时,模型的一些能力只在某一个数值左右浮动(特别一些能力是在0左右浮动),在模型规模大到一定程度时这些能力就会突然提升。这些能力包括多步推理、上下文理解等,这些本来都是自然语言处理研究中很难的课题,但是大模型一出现(以ChatGPT为代表),这些问题甚至都是被顺带解决的。
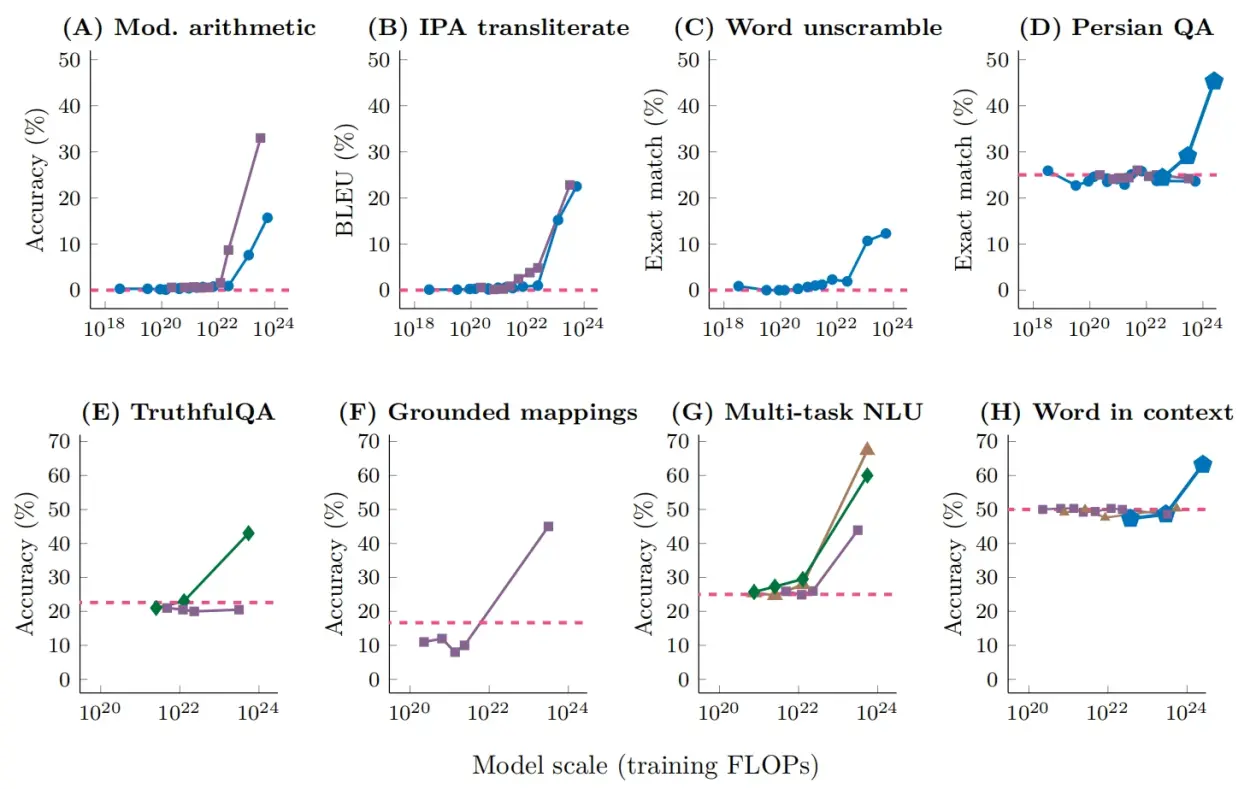
这个现象非常神奇,说明大模型和小模型可能是有根本的差异的
昨天看了一些网络文章和论文,才意识到这种现象其实不罕见的,例如我们常说的微观和宏观、温度之类的等都体现出了涌现。包括复杂系统等,都存在一些涌现现象。

2.训练过程的涌现
当然,本篇论文并不是说明上面这种随着模型规模增大而出现的涌现现象。相反,作者仅仅用了单层transformer网络,是个名副其实的小模型。本文研究的是训练过程中的涌现。
作者想要这个小模型做一个很简单的任务:同余加法,即计算(a+b)%c,可能有不懂编程的朋友,这里解释一下,a、b和c都是整数,%符号代表取模,或者说,取余数。就是先计算a+b,然后除以c,要的是余数,例如(3+3)%4=2
可能大家说,哎,这不是很简单嘛。确实,对我们来说确实很简单,但是要知道神经网络里是没有加法、取模这些操作的,这些操作是要学的。就像你要教一个婴儿加法一样,对神经网络并不是什么很简单的问题。
然后作者就开始训练了,一开始很正常的过拟合了,在训练集上表现得很好,但是测试集上性能一直提不上去。然后,突然在某个时刻,测试集的准确率直接飙升到100%,这意味着:在这一刻,网络完全学会了同余加法。这个能力就这样涌现出来了。

3.这和傅里叶变换有什么关系?
可能大家会问,哎,做同余加法怎么扯上傅里叶变换了?事实上,这个问题确实可以用傅里叶变换来做,具体可以看图:
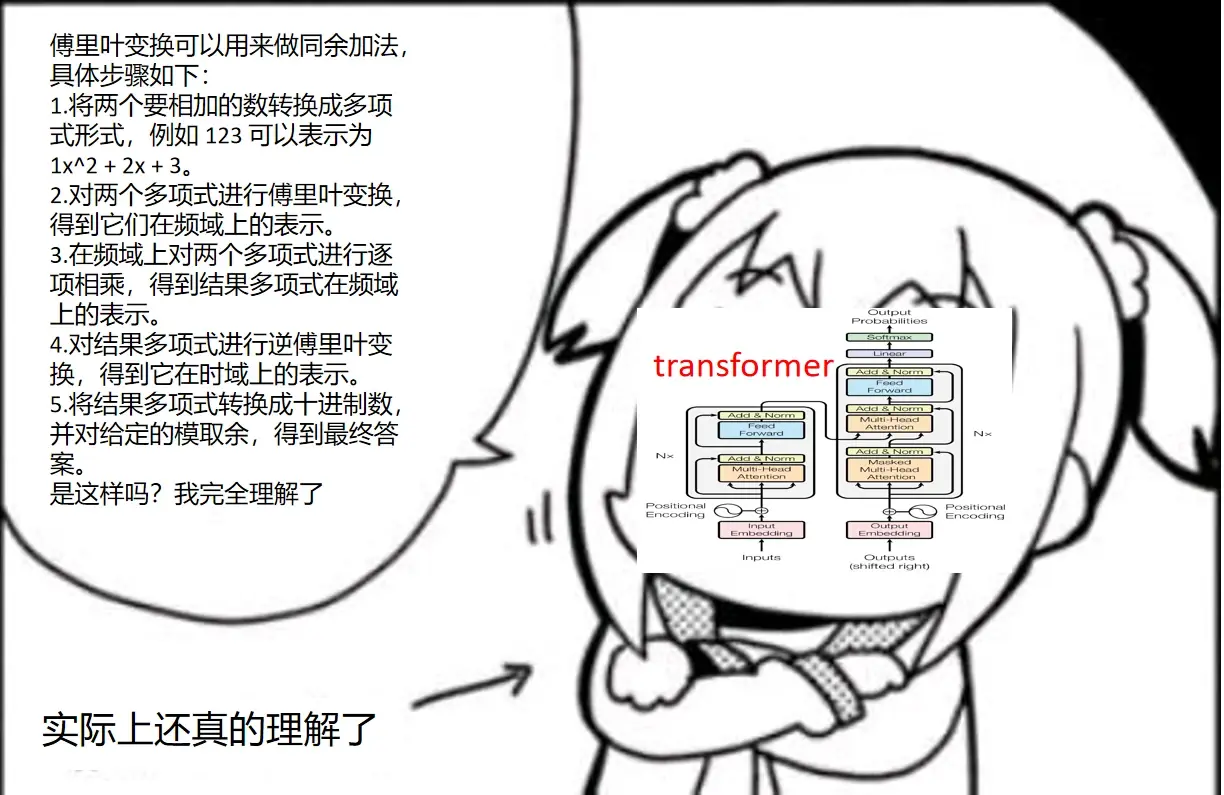
做法是new bing告诉我的(我终于有new bing beta测试资格了),高数什么的早就忘掉了。
没错,经过训练的神经网络就在某一刻突然学会了用傅里叶变换来完成同余加法,相当于直接从小学生蜕变了大学生。

4.怎么学会的
其实transformer之所以强大,是因为已经被证明是图灵完备的,所以能够算出来其实并不出人意料,但涌现是出人意料的,为什么学着学着就真的学会了傅里叶变换呢?作者可能也知道量变引起质变,这个过程一定有什么在做铺垫,于是作者尝试做了些分析。
作者用逆向工程(这部分还是挺专业的,不展开)展开了研究,认为模型学习分为了三个阶段:
(1)记忆。比较好理解,过拟合可能得主要原因是网络在记忆训练集
(2)形成电路。网络概括出了一种机制,或者说网络自己发现了规律。这时记忆仍然会影响网络性能,所以性能还达不到100%。
(3)清理。将记忆清理掉,留下比较纯粹的电路。
涌现就是在清理的过程中学会的。
这一观点某种程度上也是很像我们人类的学习的,即从一些个性中发现共性,然后带着共性去研究其他个性。
