量子计算 [ζ(1)] -- 可逆逻辑计算

在量子计算 [2].ext 里说过: 在电子计算机里, X门为NOT门, CNOT门为可逆XOR门, CCNOT门为可逆AND门, 并且通过这3个门组合可以还原任意逻辑电路.

不过yysy, 对于不熟悉可逆计算的人[比如说我]来说, 可逆计算是挺难上手的一个东西, 下面用过一个小例子来展示如何用可逆计算实现基本逻辑.

加法器

加法器是一个不算难并且有一定复杂程度的电路, 所以加法器是一个绝妙的例子.

基本介绍

普通的波纹进位加法器由一大堆全加器构成. 全加器输入3bits: A, B 和 Cin, Cin表示从上一个全加器获得的进位, 而输出2bits: S 和 Cout, S为加法的结果, Cout为进位输出. 则一个n-bits加法器可以表示为:

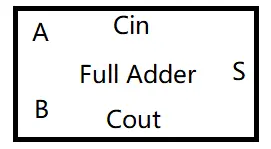
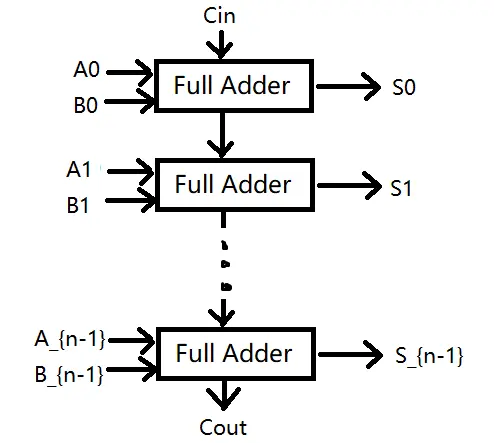
不难推断在一个全加器里: $S%3DA%5Coplus%20B%5Coplus%20C_%7Bin%7D$ 和 $C_%7Bout%7D%3D(A%5Ccdot%20B)%5Coplus(B%5Ccdot%20C)%5Coplus(A%5Ccdot%20C)$ , 其中 $%5Coplus$ 是XOR, $%5Ccdot$ 是AND. 稍微化简一下Cout得: $C_%7Bout%7D%3D(A%5Ccdot%20B)%5Coplus(C_%7Bin%7D%5Ccdot(A%5Coplus%20B))$

可逆逻辑门

可逆逻辑电路由可逆逻辑门构成, 并且可逆逻辑门输入比特数与输出比特数保持一致 [准确来说, 是输入即输出]. 所以不像传统电子电路, 可逆逻辑电路没有明显的输出. 为了做到像传统电路具有明显的输出, 可逆电路必须有一个额外的比特用于储存结果, 以XOR做例子:

可以看到可逆XOR门[即CNOT门]把输入的一个比特用作储存结果, 而可逆AND门[即CCNOT门]则是把结果作用在第3个比特上:

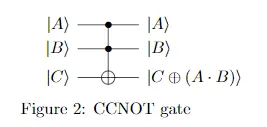
这就是说可逆逻辑门"没有明显输出"的原因, 为了做到"明显的输出"需要额外一个比特输入为 $%7C0%5Crangle$ 输出为 $%7CResult%5Crangle$ , 比如传统XOR可以表示为:

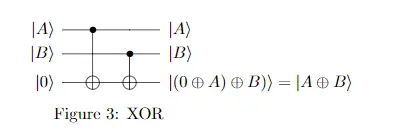
对于AND就更好办了, 在CCNOT里, 如果C=0, 那么第3比特就为 A·B

逻辑分解

不做任何优化把全加器分解为单个逻辑的形式: $T_1%20%3D%20A%20%5Coplus%20B%20%5C%5C%0A%20%20%20%20%20%20%20%20%20%20%20%20T_2%20%3D%20A%20%5Ccdot%20B%20%5C%5C%0A%20%20%20%20%20%20%20%20%20%20%20%20T_3%20%3D%20C_%7Bin%7D%20%5Ccdot%20T_1%20%5C%5C%0A%20%20%20%20%20%20%20%20%20%20%20%20S%20%3D%20C_%7Bin%7D%20%5Coplus%20T_1%20%5C%5C%0A%20%20%20%20%20%20%20%20%20%20%20%20C_%7Bout%7D%20%3D%20T_2%20%5Coplus%20T_3$

写为电路形式为:

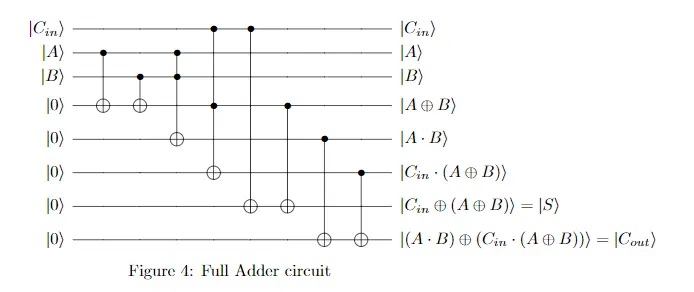
来测试一下: (使用自制的库 nyasQuantumCalculate [老推销员了])

from nyasQuantumCalculate.RevCal import *
from nyasQuantumCalculate.RevCal.Builtin import *

def FullAdder(register: Bits, Cin: bool, A: bool, B: bool):
    """返回的结果是 (S,Cout)"""
    assert len(register) == 8, "包含输入Cin,A,B, 3个临时比特, 输出S,Cout"

    # 把输入应用到寄存器上
    (X if Cin else I)(register[0])
    (X if  A  else I)(register[1])
    (X if  B  else I)(register[2])

    # 执行全加器电路
    CNOT(register[1], register[3])
    CNOT(register[2], register[3])

    CCNOT(register[1], register[2], register[4])

    CCNOT(register[0], register[3], register[5])

    CNOT(register[0], register[6])
    CNOT(register[3], register[6])

    CNOT(register[4], register[7])
    CNOT(register[5], register[7])

    # 测量比特以获得输出
    result = M(register[6]), M(register[7])
    # 记得操作完还原电路
    RA(register)

    return result


# 初始化系统
bsys = BitsSystem(8)
register = bsys.getBits()

# 历遍所有输入
print("Cin A B | S Cout")
for c in range(2):
    for a in range(2):
        for b in range(2):
            result = FullAdder(register, bool(c), bool(a), bool(b))
            print(f" {c}  {a} {b} | {int(result[0])}  {int(result[1])}")

#Cin A B | S Cout
# 0  0 0 | 0  0
# 0  0 1 | 1  0
# 0  1 0 | 1  0
# 0  1 1 | 0  1
# 1  0 0 | 1  0
# 1  0 1 | 0  1
# 1  1 0 | 0  1
# 1  1 1 | 1  1

Can we do betttttter?

Sure. 如果没要求在运算过程里保持输入比特不变的话, 则把临时结果与输入合拼到一起得到:

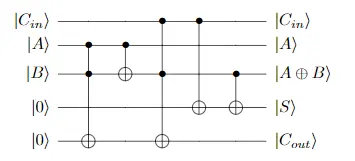
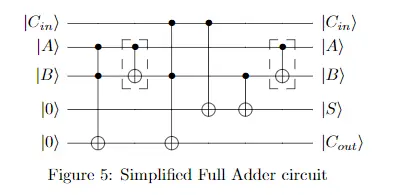
最后找到数据位[也就是输入比特]被修改的位门, 并反向作用这些位门[ $(CBA)%5E%7B-1%7D%3DA%5E%7B-1%7DB%5E%7B-1%7DC%5E%7B-1%7D$ ], 得到最后的全加器:

修改FullAdder函数, 再试着自己测试:

def FullAdder(register: Bits, Cin: bool, A: bool, B: bool):
    """返回的结果是 (S,Cout)"""
    assert len(register) == 5, "包含输入A,B,Cin, 输出S,Cout"

    # 把输入应用到寄存器上
    (X if Cin else I)(register[0])
    (X if  A  else I)(register[1])
    (X if  B  else I)(register[2])

    # 执行全加器电路
    CCNOT(register[1], register[2], register[4])
    CNOT(register[1], register[2])
    CCNOT(register[0], register[2], register[4])
    CNOT(register[0], register[3])
    CNOT(register[2], register[3])
    CNOT(register[1], register[2])

    # 测试数据比特通过电路后是否没有改变
    assert MA(register[:3]) == [Cin, A, B]
    # 测量比特以获得输出
    result = MA(register[3:])
    # 记得操作完还原电路
    RA(register)

    return result

组合全加器

以3-bits加法器为例, 通过组合全加器, 则加法器电路为:

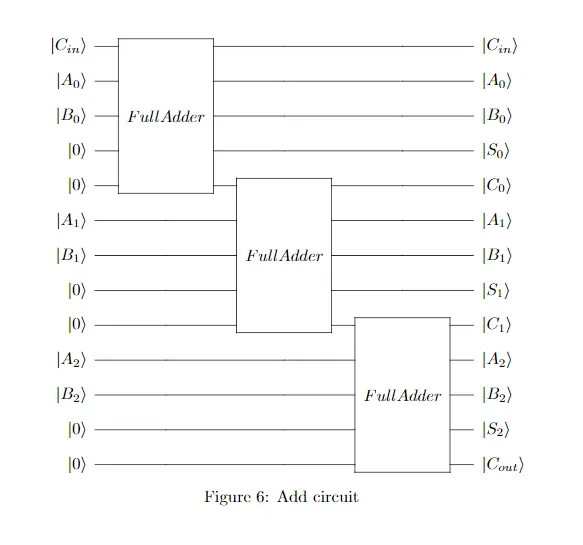
可以注意到, 在单个全加器里, 进位输入是第一个比特, 进位输出是最后一个比特, 所以可以排列成这么规则的形状, 不然需要插入大量的SWAP [虽然排得这么整齐对写代码没有明显的好处], 并且对于n-bits加法器, 一共需要 4*n + 1 bits

把FullAdder函数包装成黑箱, 再测试一下

from nyasQuantumCalculate.RevCal import *
from nyasQuantumCalculate.Utils import Bools2Int, Int2Bools


def FullAdder(register: Bits) -> None:
    assert len(register) == 5
    Builtin.CCNOT(register[1], register[2], register[4])
    Builtin.CNOT(register[1], register[2])
    Builtin.CCNOT(register[0], register[2], register[4])
    Builtin.CNOT(register[0], register[3])
    Builtin.CNOT(register[2], register[3])
    Builtin.CNOT(register[1], register[2])


# 初始化系统
n = 3       # 测试 n-bits 加法器
bsys = BitsSystem(4 * n + 1)
A_register = bsys[1::4]
B_register = bsys[2::4]
S_register = bsys[3::4] + bsys[-1]      # 最后一个全加器的Cout也属于输出数字


def Add(a: int, b: int) -> int:
    # 检查输入数字, 不可以超过 2^n-1
    assert a < (1 << n) and b < (1 << n)

    # 把输入应用到寄存器上
    ApplyFromBools(Builtin.X, Int2Bools(a)[::-1], A_register)
    ApplyFromBools(Builtin.X, Int2Bools(b)[::-1], B_register)

    # 作用FullAdder黑箱
    for i in range(n):
        FullAdder(bsys[4*i: 4*i+5])

    # 测量输出寄存器
    result = Builtin.MA(S_register)
    # 还原bits系统
    Builtin.RA(bsys[:])
    # 把测量结果转化为int
    return Bools2Int(result[::-1])


# 简单历遍所有可能的输入
for a in range(1 << n):
    for b in range(1 << n):
        print(f"{a} + {b} = {Add(a, b)}")

运行结果就不展示了, 可以自己尝试运行一下

需要留意的是, 运算过程里只用到了可逆逻辑门, 也就是说整个过程也是可逆的, 把加法电路反着运行就可以从输出得到输入, 这是传统电子电路无法做到的.

Can we do the best?

确实, 就算是这个5bits的全加器也不是最好的方案. 以下来不严格讨论最好可以做成什么样子.

可逆逻辑过程的重点是可逆, 即从输出推导输入. 在全加器里, 必定输入3个bits: A, B, Cin 和必定输出2个bits: S, Cout. 输出少于输入, 这明显不可逆. 那么把输出增加到3bits: S, Cout, X, 其中X的逻辑未定, 这样子存在可逆电路吗. 答案也是否, 如果给出 S=1, Cout=0, 则存在3种可能的输入: {A=1, B=0, Cin=0}, {A=0, B=1, Cin=0}, {A=0, B=0, Cin=1}, 仅依靠一个额外的比特X不足以覆盖所有情况. 所以不难知道, 最好的全加器由4bits构成 [也就是输入A,B,Cin和0, 输出S,Cout,X,Y, 其中XY逻辑未定]

结语

最后, 可以自己试着设计这个4bits全加器的电路. 也欢迎大家进瑟图群讨论啦: [274767696]

nyasQuantumCalculate仓库 (已更新单独的可逆电子电路的包: RevCal): [github.com/nyasyamorina/nyasQuantumCalculate]

也许以后会出一篇这节的附章, 把4bits全加器的可逆电路介绍一下, 然后再介绍一下量子版的全加器. 不过说不定也不会做 (咕咕咕