A.定义f(x)为x的各位之和。给定一个n。求大于等于n的最小的数p,使得gcd(f(p),p)>1.
签到题。显然若p为3的倍数则一定成立。所以检验后三个就行了。
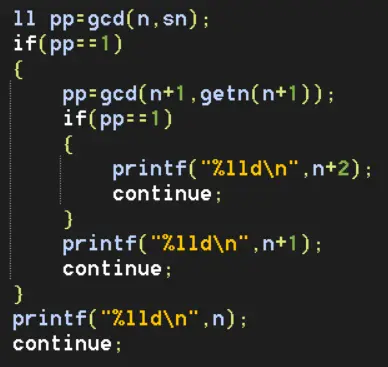
全部代码:https://pastebin.com/iC05bgZy

B.给定若干大小为n的背包。给定m个物品。保证每样物品的大小均为2的整数幂。求至少要用多少背包装下全部物品。
签到题。把物品从大到小排序。能放就放。易证这一定是最好的处理方法。
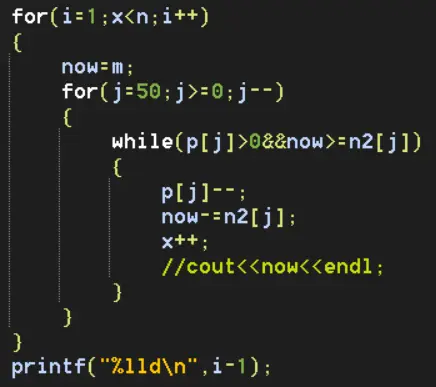
全部代码:https://pastebin.com/sMXMf8ra

C.给定n块平行的平面镜子。每次一束强度为k的光穿过镜子,将同时反射出一束强度为k-1的光往反方向照射。强度为0的光会直接消散。强度>0且前方没有镜子的光将射向外界。初始时有一束强度为p的光从最左侧射入,求最终射向外界的光的总数。
dp。光强为k的光,在前方还有x面镜子(也即后方还有n-x面镜子)时,将等效于前方还有x-1面镜子的光强k的光+前方还有n-x面镜子的光强k-1的光。即:令dp[i][j]为光强i,前方还有j面镜子。则有dp[i][j]=dp[i][j-1]+dp[i-1][n-j];
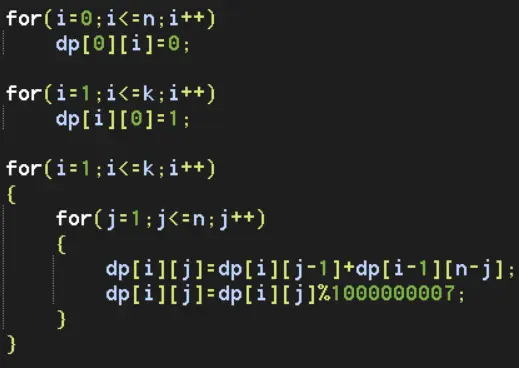
全部代码:https://pastebin.com/TUbFVYGt

D.给定初始k=0,对k进行加法或乘法运算。每回合给定3个数a,b,c。a决定这回合是加法还是乘法。b是加数或乘数。c是可以加或者乘的次数。每次运算完后向上取整。给定m,问从1-m中的每一个数,需要至少多少次回合才能够达到?如果不可能达到则输出-1。
显然如果我们完全模拟一遍,需要mn^2的复杂度,这是不可接受的。但是我们发现,如果a,b全部固定,且c=1,那么每一个数在该回合都只有一种到达的方式。举个例子:如果a=1,b=1,那么在本回合,3显然只有由2得来。即便此时还有c=4,3可以由1→2→3得到,但我们最后一步永远是通过2→3得到的。由此可以将它看做一个dp。dp传递的是我还可以变化几次。在每一回合中,对于已经得到的数,我还可以变化c次;而对于刚刚得到的数,我们还可以变化刚刚的变化数-1次。更抽象的说,我们可以把数组看做几棵树,因为在每个回合,我们都能保证每个点至多只有一个父节点和一个子节点。复杂度仅为mn。
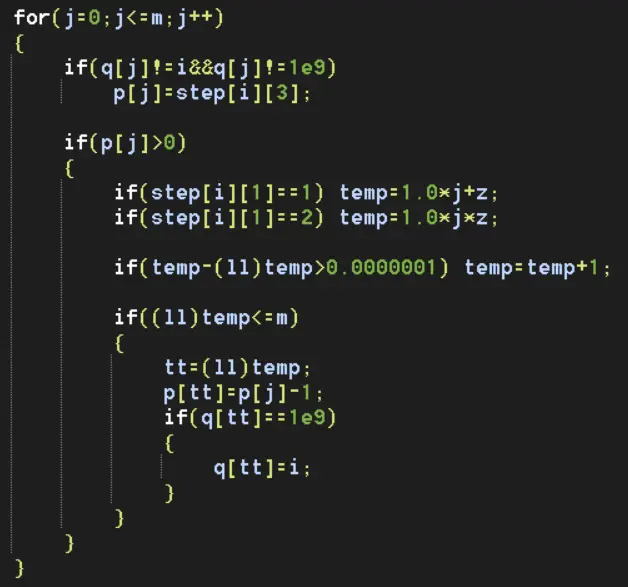
if(q[j]!=i&&q[j]!=1e9):若这个数不是这回合刚刚得到的,且这个数是可以得到的。那么我们把它的剩余次数改为c。(因为它肯定在之前的回合得到了。)
if(p[j]>0):如果到达这个数时,还能有剩余的操作次数的话。
全部代码:https://pastebin.com/XX4s49Y2

E.给定n个点。这n个点构成了一个有向完全图。然而你不知道每条边的方向。给你每个点的入度。你现在可以询问点A和点B。如果A可以到达B,那么会回复Yes,否则回复No。你可以询问无限次,但是如果你拿到的回复是Yes,你必须立刻终止询问。你最终需要给出的答案是两个点。我们定义点A和点B的距离是A的入度-B的入度。请你给出两个点,使得两点距离最大。答案必须遵循三条准则:
你的答案必须符合给你的每个点的入度。
你的答案必须符合给你的所有回复。
不能有别的答案满足以上条件且比你的更大。
只要满足这三个条件,任何答案都算是正确的。
从距离最大的两点开始问起,遇到Yes输出这两点即可。因为你的图是任意构造的。如果入度大的点都能到入度小的点,很容易构造出入度小的点到入度大的点的路径。
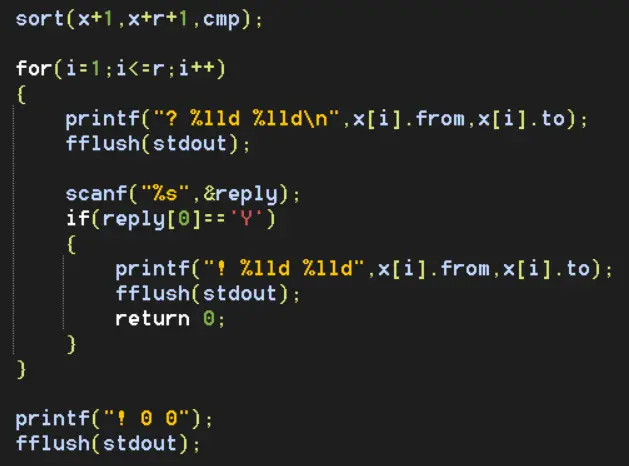
全部代码:https://pastebin.com/EH3wqLqH

F.给定一颗树。每个结点上有ai个礼物。给定k。Alice和Bob轮流操作,每次选择一个点,将该节点上任意数量的礼物移动至它的第k个祖先。不能选择没有第k个祖先的点。不能选择没有礼物的点。不能移动的人输。每个点都有可能是根节点,求当每个点作为跟节点的时候,胜负的情况。
这道题没做出来,仅提供思路:
这是一个NIM博弈。
这是一个阶梯NIM博弈。
考虑某个确定了根节点的情况,则深度为0,k,2k,3k...的点形成一个阶梯博弈,深度为1,1+k,1+2k,1+3k...的点形成了一个阶梯博弈,以此类推。可算出每个阶梯博弈的SG函数值。最终得到当前博弈总结果。
如果每次换节点都重新考虑的话时间复杂度为n^2,是不可接受的。进行优化。我们发现阶梯博弈中,偶数阶是无所谓的。所以我们把树分为两部分:偶数点和奇数点。也就相当于用两种颜色给树染色,使得任意相邻节点颜色均不同。这样,每次切换根节点的时候,我们只需要维护更换的两个点即可。这样执行两次把偶部分和奇部分都处理掉即可。
