比赛链接：https://codeforces.com/contest/1495 https://codeforces.com/contest/1496

官方题解：https://codeforces.com/blog/entry/88533

难度：Div1&2

Div2A Split it!

题意：给定一个长度为 $n$ 字符串 $s$ 与 $k$ ，问这个字符串能否划分为 $s%3Da_1%2Ba_2%2B%5Cdots%2Ba_k%2Ba_%7Bk%2B1%7D%2BR(a_k)%2BR(a_%7Bk%E2%88%921%7D)%2B%E2%80%A6%2BR(a_1)$ 的形式，其中 $R(x)$ 表示将串 $x$ 反转得到的字符串。

题解：易得 $a_1%2Ba_2%2B%5Cdots%2Ba_k$ 与 $R(a_k)%2BR(a_%7Bk%E2%88%921%7D)%2B%E2%80%A6%2BR(a_1)$ 是互为反转的串，中间需要插入一个 $a_%7Bk%2B1%7D$ 。找到 $s$ 中最长互为反转的前后缀长度，然后与 $k$ 作比较即可。注意特判 $a_%7Bk%2B1%7D$ 为空串的情况，时间复杂度 $O(n)$ 。

#include <bits/stdc++.h> //code by cjj490168650
using namespace std;

const int N=110;

int T,n,k;
char s[N];

int main()
{
    scanf("%d",&T);
    while (T--)
    {
        scanf("%d%d",&n,&k);
        scanf("%s",s+1);
        int l=1,r=n;
        while (l<r && s[l]==s[r]) l++,r--;
        if (k+k==n) printf("NO\n");
        else if (l>k) printf("YES\n");
        else printf("NO\n");
    }
    return 0;
}

Div2B Max and Mex

题意：定义 $%5Cmax(S)$ 为集合 $S$ 中的最大值， $%5Ctext%7Bmex%7D(S)$ 为集合 $S$ 中未出现的最小非负整数。给定 $S$ 的初始情况，然后执行 $k$ 次将 $%5Clceil%5Cfrac%7B%5Cmax(S)%2B%5Ctext%7Bmex%7D(S)%7D%7B2%7D%5Crceil$ 插入 $S$ 中的操作，求 $S$ 中最后有多少个互不相同的数。

题解：初始时若 $%5Cmax(S)%3C%5Ctext%7Bmex%7D(S)$ ，此时必有 $S%3D%5C%7B0%2C1%2C2%2C...%2Cn-1%5C%7D$ ， $%5Cmax(S)%3Dn-1$ ， $%5Ctext%7Bmex%7D(S)%3Dn$ ， $%5Clceil%5Cfrac%7B%5Cmax(S)%2B%5Ctext%7Bmex%7D(S)%7D%7B2%7D%5Crceil%3Dn$ ，则每次执行插入操作都会将 $%5Ctext%7Bmex%7D(S)$ 插入，最终 $S$ 中会增加 $k$ 个数。初始时若 $%5Cmax(S)%3E%5Ctext%7Bmex%7D(S)$ ，则必有 $%5Ctext%7Bmex%7D(S)%3C%5Clceil%5Cfrac%7B%5Cmax(S)%2B%5Ctext%7Bmex%7D(S)%7D%7B2%7D%5Crceil%5Cle%5Cmax(S)$ ，此时插入操作并不会改变 $%5Ctext%7Bmex%7D(S)$ 与 $%5Cmax(S)$ ，因此最终 $S$ 中最多增加 $1$ 个数。我的代码中使用了 set 求 $%5Ctext%7Bmex%7D(S)$ ，时间复杂度 $O(n%5Clog%20n)$ ，如果使用哈希表，则复杂度可降为 $O(n)$ 。

#include <bits/stdc++.h> //code by cjj490168650
using namespace std;

const int N=100010;

int T,n,k,x;

int main()
{
    scanf("%d",&T);
    while (T--)
    {
        scanf("%d%d",&n,&k);
        set<int>s;
        for (int i=1;i<=n;i++)
        {
            scanf("%d",&x);
            s.insert(x);
        }
        int a=*s.rbegin(),b=0;
        while (s.count(b)) b++;
        if (b==a+1)
        {
            printf("%d\n",b+k);
        }
        else
        {
            if (k) s.insert((a+b+1)/2);
            printf("%d\n",(int)s.size());
        }
    }
    return 0;
}

Div2C/Div1A Diamond Miner

题意： $x$ 轴上有 $n$ 个点， $y$ 轴上有 $n$ 个点，将 $x$ 轴上的点一一对应地向 $y$ 轴上的点连线，求连出的线段长度总和最小是多少。

题解：贪心，每次将 $x$ 轴上离原点最近的点与 $y$ 轴上离原点最近的点相连即可，证明建议看官方题解。时间复杂度 $O(n%5Clog%20n)$ 。

#include <bits/stdc++.h> //code by cjj490168650
using namespace std;

const int N=200010;

int T,n,x,y;

int main()
{
    scanf("%d",&T);
    while (T--)
    {
        scanf("%d",&n);
        vector<int>xa,ya;
        for (int i=1;i<=n+n;i++)
        {
            scanf("%d%d",&x,&y);
            if (x==0) ya.push_back(abs(y));
            else xa.push_back(abs(x));
        }
        sort(xa.begin(),xa.end());
        sort(ya.begin(),ya.end());
        double ans=0;
        for (int i=0;i<n;i++)
        {
            double x=xa[i],y=ya[i];
            ans+=sqrt(x*x+y*y);
        }
        printf("%.15lf\n",ans);
    }
    return 0;
}

Div2D/Div1B Let's Go Hiking

题意：有 $n$ 个格子排成一排，每个格子有一个高度，高度各不相同。甲首先选择一个起点，然后乙再选择一个起点，然后甲乙两人轮流移动。每次可以往左或往右移动一格，甲只能往比当前位置低的格子移动，乙只能往比当前位置高的格子移动。轮到某人时如果他不能移动，则对方获胜。若两人都采取最优策略，问甲要获胜的话有多少种起点选择方案。

题解：首先可以知道，甲的起点必须选在可以往左右两边走的位置，即“山顶”。因为如果甲的起点只能往一个方向上走，那么乙在那个方向上更低一格堵住甲即可获胜。

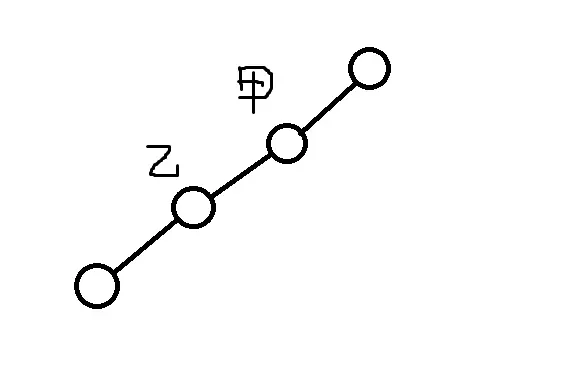
当甲选择某个山顶作为起点后，乙的选择可以有以下两种情况：

乙从某个“山脚”出发，往甲不在的“山顶”移动。此时甲乙两人的路线互不影响，找到乙能走的最长路线和甲能走的最长路线对比即可。

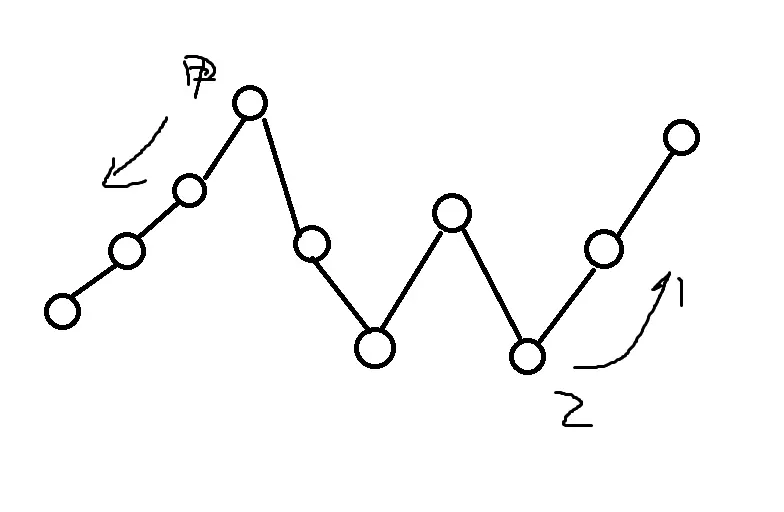
乙从甲附近的“山坡”出发，往甲所处的“山顶”移动。此时乙所选的位置与甲的距离不能为偶数，否则甲就可以往乙的方向上走从而堵住乙。当乙按正确策略选择起点后，甲不能往乙的方向上走，否则会被乙堵住。两者路线确定后比较长度即可。

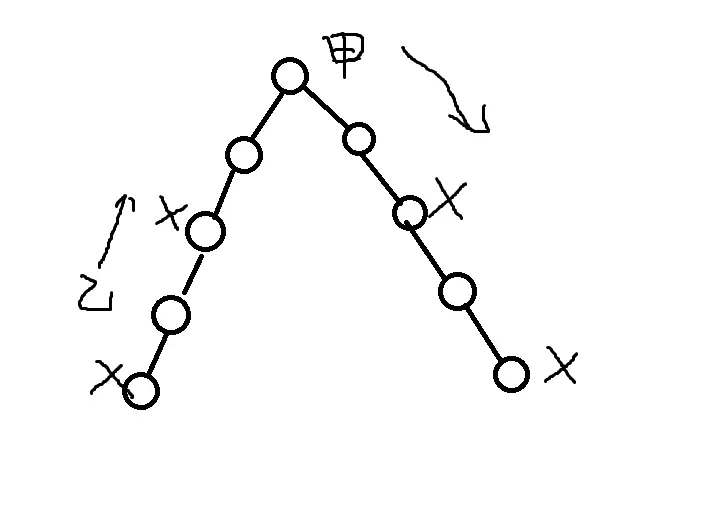
对于每个山顶，判断甲以该山顶为起点时，乙能否有策略战胜甲，若没有则甲可获胜，更新答案。时间复杂度 $O(n)$ 。（补充：事实上，如果甲想要获胜，那么他的起点必须选在下山路径最长的“山顶”上，因此答案只有 $0$ 或 $1$ 。）

#include <bits/stdc++.h> //code by cjj490168650
using namespace std;

const int N=100010;

int n,p[N];
int dl[N],dr[N],ul[N],ur[N];
int pre[N],nxt[N];
int maxl[N],maxr[N];

int main()
{
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
    {
        scanf("%d",&p[i]);
    }
    for (int i=2;i<=n;i++)
    {
        if (p[i]>p[i-1]) dl[i]=dl[i-1]+1;
        else ul[i]=ul[i-1]+1;
    }
    for (int i=n-1;i>=1;i--)
    {
        if (p[i]>p[i+1]) dr[i]=dr[i+1]+1;
        else ur[i]=ur[i+1]+1;
    }
    int t=1;
    for (int i=1;i<=n;i++)
    {
        if (dl[i] && dr[i]) pre[i]=t;
        if (ul[i] && ur[i]) t=i;
        maxl[i]=max(maxl[i-1],max(ul[i],ur[i]));
    }
    t=n;
    for (int i=n;i>=1;i--)
    {
        if (dl[i] && dr[i]) nxt[i]=t;
        if (ul[i] && ur[i]) t=i;
        maxr[i]=max(maxr[i+1],max(ul[i],ur[i]));
    }
    int ans=0;
    for (int i=1;i<=n;i++)
    {
        if (!dl[i] || !dr[i]) continue;
        if (maxl[pre[i]-1]>=max(dl[i],dr[i])) continue;
        if (maxr[nxt[i]+1]>=max(dl[i],dr[i])) continue;
        if (ul[pre[i]]>=max(dl[i],dr[i])) continue;
        if (ur[nxt[i]]>=max(dl[i],dr[i])) continue;
        int tl=ur[pre[i]]; if (!(tl&1)) tl--;
        int tr=ul[nxt[i]]; if (!(tr&1)) tr--;
        if (dr[i]>tl && dl[i]>tr) ans++;
    }
    printf("%d\n",ans);
    return 0;
}

Div2E/Div1C Garden of the Sun

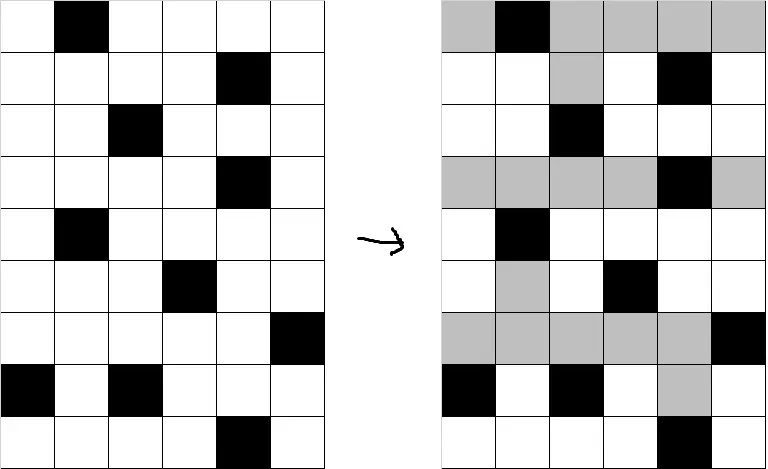
题意：给定一个花园，表示为 $n$ 行 $m$ 列的矩阵。花园内有的位置种了花，有的位置为空地，初始时每个空地周围的八个格子不会有别的空地。现需要挖出更多空地，使得原本为空地的位置互相连通，且最终空地不会形成环路。构造一组满足条件的方案。

题解：每隔两行将一整行都变成空地，行与行之间找合适的位置相连，注意边界位置的处理。

#include <bits/stdc++.h> //code by cjj490168650
using namespace std;

const int N=510;

int T,n,m;
char s[N][N],ans[N][N];
int l[N];

void init()
{
    for (int i=1;i<=n;i++)
    {
        for (int j=1;j<=m;j++)
        {
            ans[i][j]=0;
        }
    }
}

int main()
{
    scanf("%d",&T);
    while (T--)
    {
        init();
        scanf("%d%d",&n,&m);
        for (int i=1;i<=n;i++)
        {
            scanf("%s",s[i]+1);
            l[i]=m;
            for (int j=1;j<=m;j++)
            {
                if (s[i][j]=='X')
                {
                    ans[i][j]='X';
                    l[i]=min(l[i],j);
                }
                else ans[i][j]='.';
            }
        }
        for (int i=1;i<=n;i+=3)
        {
            for (int j=1;j<=m;j++) ans[i][j]='X';
            if (i+3<=n)
            {
                int t=min(l[i+1],l[i+2]);
                ans[i+1][t]='X';
                ans[i+2][t]='X';
            }
            else if (i+2==n)
            {
                for (int j=1;j<=m;j++)
                {
                    if (s[n][j]=='X') ans[n-1][j]='X';
                }
            }
        }
        for (int i=1;i<=n;i++)
        {
            printf("%s\n",ans[i]+1);
        }
    }
    return 0;
}

后面的题目暂未解决。

Codeforces Round #706 个人题解

Div2A Split it!

Div2B Max and Mex

Div2C/Div1A Diamond Miner

Div2D/Div1B Let's Go Hiking

Div2E/Div1C Garden of the Sun