阅前UP提醒:不熟悉《弹丸论破》的读者阅读本文较难,阅读本文是最好自行脑补《弹丸论破V3》的界面,没阅读过[#4]的观众请先去阅读(链接:CV21231462),请继续下滑开始正文
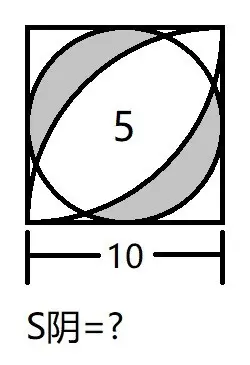
前情回顾:
CA和CB都是⊙C的半径
则∵CA=10,CB=10
∴CA=10=CB
∴CO=√(50)
nice!又多了一个已知条件!

思考程序重启......
启动成功......

再看看别的吧
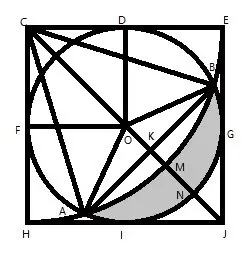
————开始思考————
言弹: ① 垂直平分线 ② 勾股定律 ③ 同圆或等圆的半径相等
10 前面已经这证明出CA=CB和OA=OB了
9 想想看还要求什么......
8 之前说过要求CO,AB和OK
7 现在已经求出了CO=√(50)
6 AB的中点是K
5 那求AB的话可以先做个假设:AK=BK
4 那OK呢......
3 OK在三角形OAB中
2 OK连接了三角形OAB的一个角和这个角的对边
1 OK不太好求,应该先求AB
那该怎么求AB呢......(从头开始)
—————————————————————————————————————————
[用言弹①同意AK=BK]BREAK

前面证明出了CA=CB和OA=OB
那就可以得出:C和O在AB的垂直平分线上
而J刚好在CO的延长线上
所以CJ垂直平分AB
那就成功证明出了AK=BK
(顺便还可以得出......)
① CO=NO
② ∠AKC=90°
③ OK=NK
—————————————————————————————————————————
[选择选项②]解

AB是一条线段,同时也是平角
则角度为180°
而∠AKC=90°
那∠BKC=90°
则可得知:三角形CAK,三角形OAK,三角形CBK和三角形OBK都是直角三角形
————开始思考————
言弹:① 10 ② √(50)③ 5 ④ 5/2
4 证明了这些是直角三角形接下来求边就方便了
3 但好像有个问题......
2 如果依靠直角三角形来求边长的话那至少要知道其中两条边的准确值
1 而现在知道的边无论是哪个直角三角形只够一条
应该有什么方法......(从头开始)
—————————————————————————————————————————
[用言弹②驳倒如果依靠直角三角形来求边长的话那至少要知道其中两条边的准确值]BREAK


也许不一定
再看下图......
有点乱
OD和OF可以不要了
搞定!
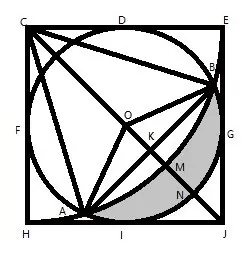
看三角形OAK和三角形OBK应该不行
这两个三角形只知道一条斜边的值是5
两条直角边是完全不知道的
那就看看三角形CAK和三角形CBK
这两个三角形是全等的
判定方式有SAS和HL
那就先只看三角形CAK吧
三角形CAK有三条边,分别是CA,CK和AK
关于三角形CAK现在只知道了CA=10和CO=√(50)
而CK只知道了一部分,那就是CO
那CK=CO+OK
那三角形CAK的三边就可以用条式子列出等量关系:
(CA)^2=(CK)^2+(AK)^2=(CO+OK)^2+(AK)^2
把已知的数字补充上去
得:10^2=(√(50)+OK)^2+(AK)^2
简化后得:50=√(200)OK+(OK)^2+(AK)^2
三角形OAK也试着用这个思路吧
已知的仅有OA=5
列出式子:
(OA)^2=(OK)^2+(AK)^2
带入已知数,得:
25=(OK)^2+(AK)^2
现在将刚刚的两条式子组成一个方程组
{ 50=√(200)OK+(OK)^2+(AK)^2 ①
{ 25=(OK)^2+(AK)^2 ②
用式子①减去式子②
得:25=√(200)OK
解得OK=5/√(8)
将结果带入式子②,得:
25=(5/√(8))^2 +(AK)^2
解得:AK=√(21.875)
很好!
又解出了几个条件
感觉很快就能得出答案了!

思考程序休止......
